最小全域木 (Minimum spanning tree) を解くアルゴリズムであるプリム法をpythonで実装したメモです。
pythonコードとアルゴリズムの流れを簡単にメモしています。
コード
def prim(G):
"""
G: 隣接グラフ
G := [ [(v_0, cost_0), (v_1,cost_1),..], [(v_2, cost_2)],...]
返り値 ans :最小全域木の重みの総和
"""
ans = 0 #答えの初期値
V = len(G) #頂点数
used = [False for i in range(V)] #探索済/未探索かを判定
#出発地点(番号0)を初期化
used[0] = 1
que = [(cost, v) for v,cost in G[0]]
heapq.heapify(que)
while que:
cost_v, v = heapq.heappop(que)
if used[v] == 1:
continue
used[v] = 1 #vを探索済みにする
ans += cost_v
for nxt, cost_nxt in G[v]:
if used[nxt] == True:
continue
heapq.heappush(que, (cost_nxt, nxt))
return ansヒープ構造を使っているので、計算量は $O(E \ \mathrm{log}(V))$ となっている。
探索過程の可視化
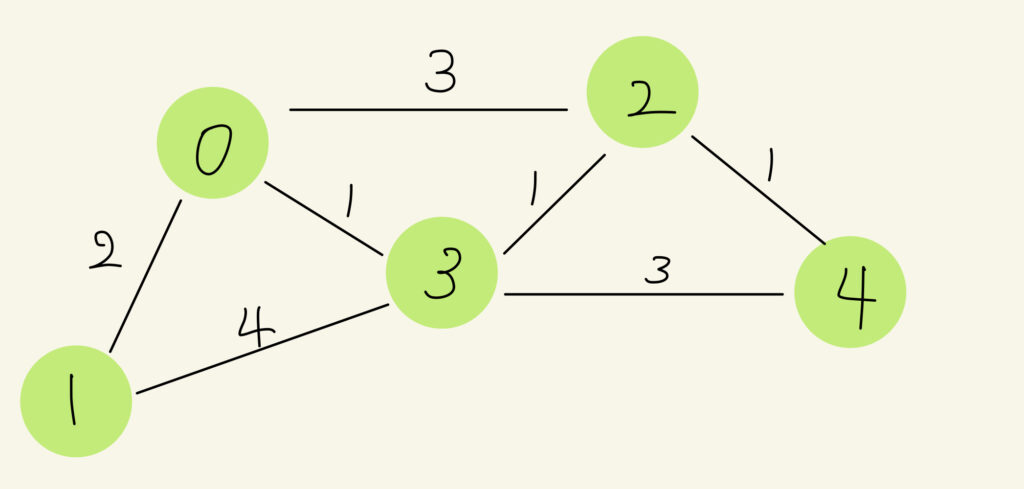
以下のような5つの頂点で構成されるグラフを考える。緑の丸が頂点で、0から4までの番号をふってある。また、辺の数字が cost を意味している。
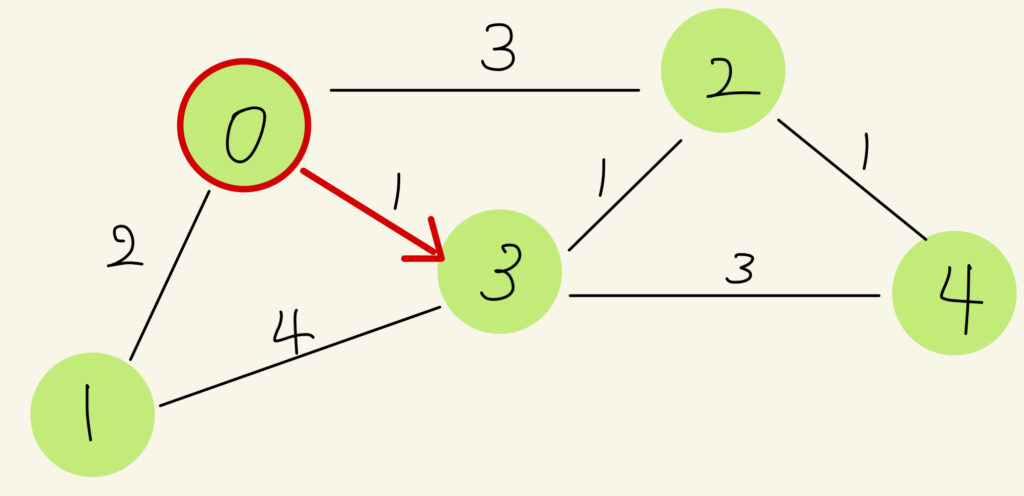
0の頂点をスタート地点とする。0に繋がる3つの辺のうち、コストが最小値1の辺(0と3を結ぶ辺)を採用する。以後、探索済みの頂点・辺は赤で示す。
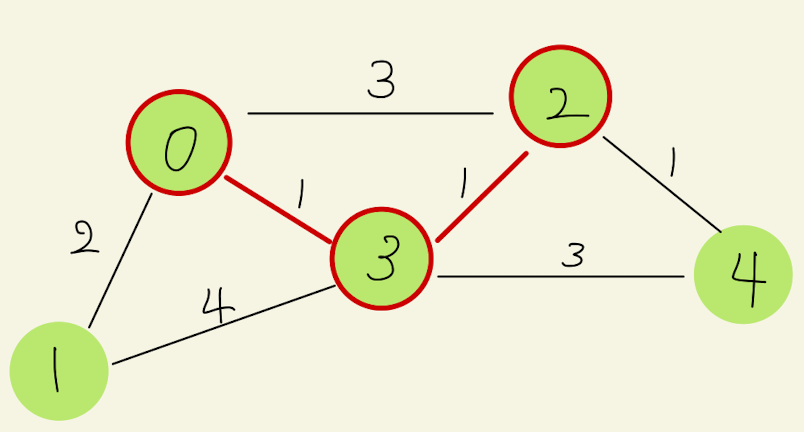
次は、探索済みの頂点0と3に隣接する頂点のうち、コストが最小のものを選ぶ。最小コストの辺は頂点3と頂点2を結ぶ辺であるため、これを探索済みにする。
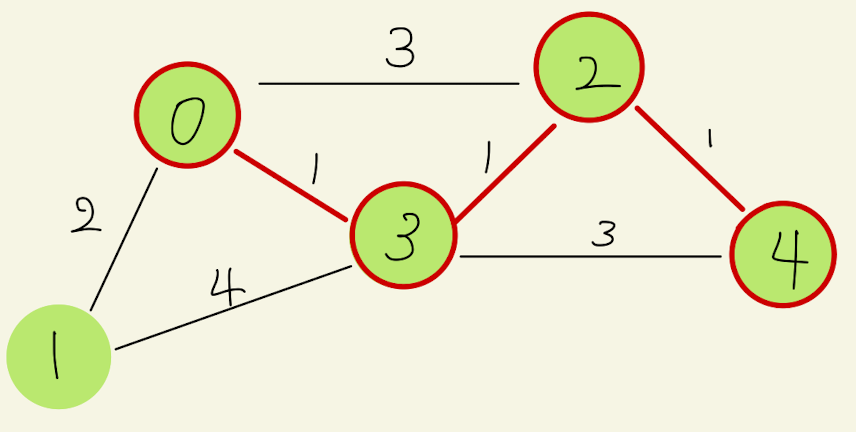
次は、頂点0, 2, 3 に隣接する辺のうちで最小コストのものを選ぶ。最小コストの辺は頂点2と頂点4を結ぶ辺であるため、これを探索済みにする。
最後は、頂点0, 2, 3, 4 に隣接する辺のうちで最小コストのものを選ぶ。最小コストの辺は頂点0と頂点1を結ぶ辺であるため、これを探索済みにする。
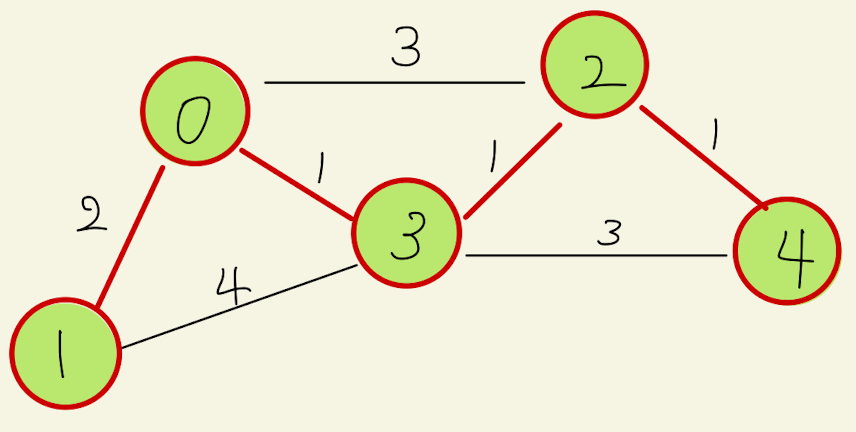
以上で最小全域木が完成し、コストは 5 であることがわかった。
以上のグラフをコードで解くと以下のようになります。
#図1を隣接グラフで書いたものがG
G = [[(1, 2), (2, 3), (3, 1)], [(0, 2), (3, 4)], [(0, 3), (3, 1), (4, 1)], [(0, 1), (1, 4), (2, 1), (4, 3)], [(2, 1), (3, 3)]]
ans = print(G)
print(ans)
#5まとめ
プリム法を用いた最小全域木の実装をメモしました。
上記のコードは AIZU ONLINE JUDGE ALDS1_12_A で正解になることを確認しています。
参考
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年
また、最小全域木の解法として、プリム法以外にもクラスカル法があります。私の過去の記事でもまとめているので、ご興味があればご覧ください。



コメント