クラスカル法 (Kruskal method) は最小全域木を解く有名なアルゴリズムです。本記事では、
- pythonのコード
- 簡単なグラフを用いた実行例
についてまとめます。特に実行例では、for文の各辺への操作を一つ一つ丁寧に取り上げています。そのため、初めて勉強する人はアルゴリズムの流れをイメージしやすいと思います。
ポイント
- Union-Find木を利用
- 計算量は $O(E \ \mathrm{log}(V))$ ($E$ は辺の本数、$V$ は頂点数)
pythonのコード
このアルゴリズムは『最初バラバラな頂点を、辺の重みが小さい順に繋げていって、一つのグループにまとめる』という流れで進んでいきます。
# Kruskal法のアルゴリズムの本体
def kruskal(Edges, V):
"""
入力
Edges: (weight, (From_node, To_node))を管理するリスト
V: 頂点数
出力
ans: 最小全域木の重み
"""
Edges.sort() #重みが小さい順に辺をソートする
ans = 0 #最小全域木の重み
uf = UnionFind(V) #UnionFindを初期化. 初期は全頂点が異なるグループ
for w, (From, To) in Edges:
#同じグループ(木)に属する場合、その辺は無視する
if uf.isSame(From, To):
continue
#異なるグループの場合、その辺を採用し、頂点From, Toを同じグループにする
else:
ans += w
uf.unite(From, To)
return ans
#=======以下、Union-Find木 各頂点の管理に利用===============
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1 for i in range(n)]
self.size = [1]*n
def root(self, x):
if self.parents[x] == -1:
return x
else:
self.parents[x] = self.root(self.parents[x]) #工夫2: 経路圧縮
return self.parents[x]
def isSame(self, x, y):
if self.root(x)==self.root(y):
return True
else:
return False
def unite(self, x, y):
x = self.root(x)
y = self.root(y)
if x==y:
#なにもしない
return
#工夫1: サイズによる合併(小さい方を大き方に合併)
if self.size[x] < self.size[y]:
x, y = y, x #yが小さい方になるように交換する
self.parents[y] = x #yの根をxに変更
self.size[x] += self.size[y]Union-Find木の実装に関しては、私の過去の記事を利用しています。興味があればご覧ください。
アルゴリズムの流れを確認
以下のグラフを用いてクラスカル法のアルゴリズムの流れを確認します。

このグラフの辺を管理するリスト Edges は以下の通りです。この Edges は重みが小さい順にソートされています。
#(重み, (出発ノード, 行き先ノード) )として管理
Edges = [(1, (0, 3)), (1, (2, 3)), (1, (2, 4)), (2, (0, 2)), (3, (0, 1)), (3, (3, 4)), (4, (1, 3))]例えば、先頭の (1,(0,3)) は、頂点0と頂点3の間の辺の重みが 1 であることを示しています。
1番目の辺
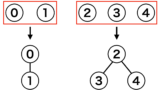
(1,(0,3)) をみると、頂点0と頂点3は異なるグループのため、両頂点を繋ぎます。
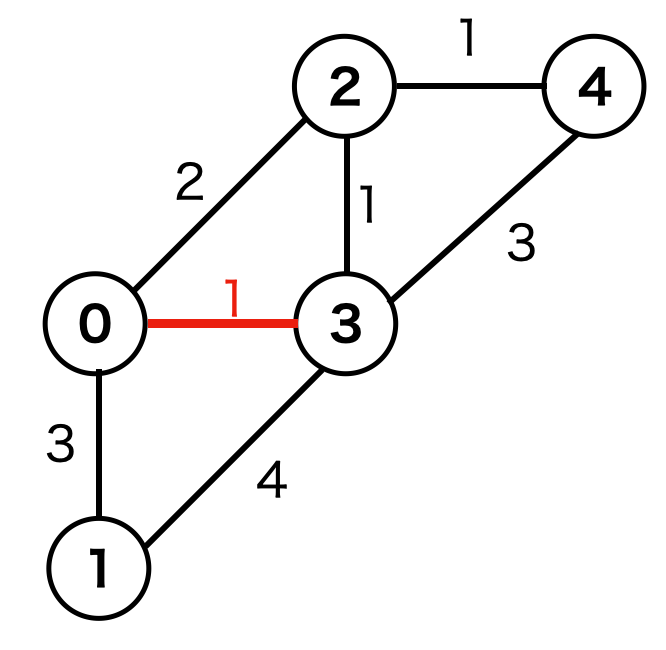
2番目の辺
(1, (2, 3)) をみると、頂点2と頂点3は異なるグループのため、両方を繋ぎます。
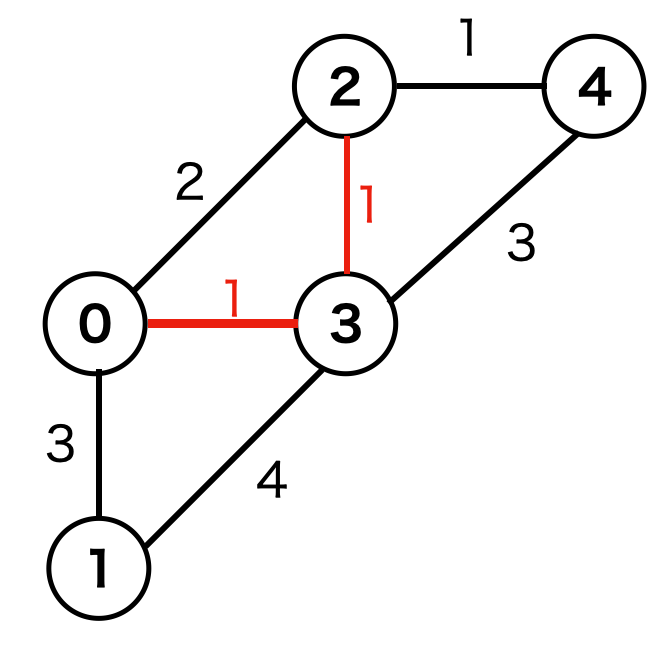
3番目の辺
(1, (2, 4)) を注目し、頂点2と頂点4をつなぎます。
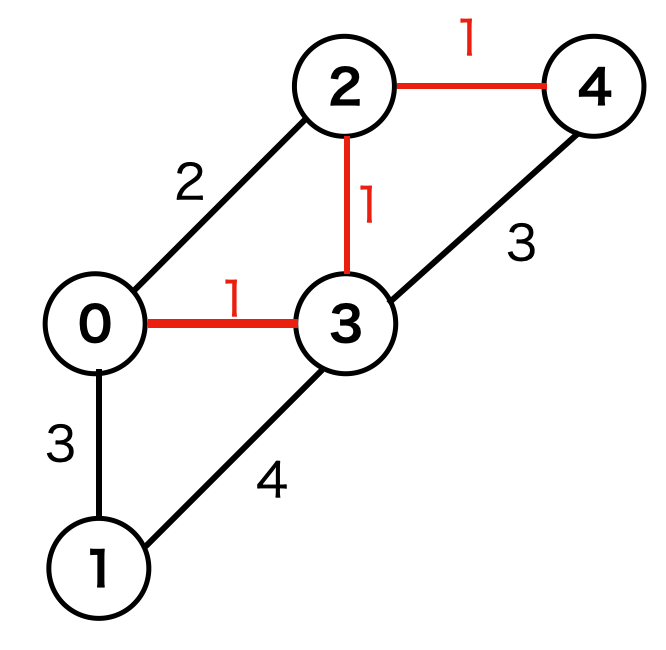
4番目の辺
(2, (0, 2)) を注目します。しかし、頂点0と頂点2は既に同じグループに属している (uf.isSame(0,2)=True) ため、この辺は採用しません。
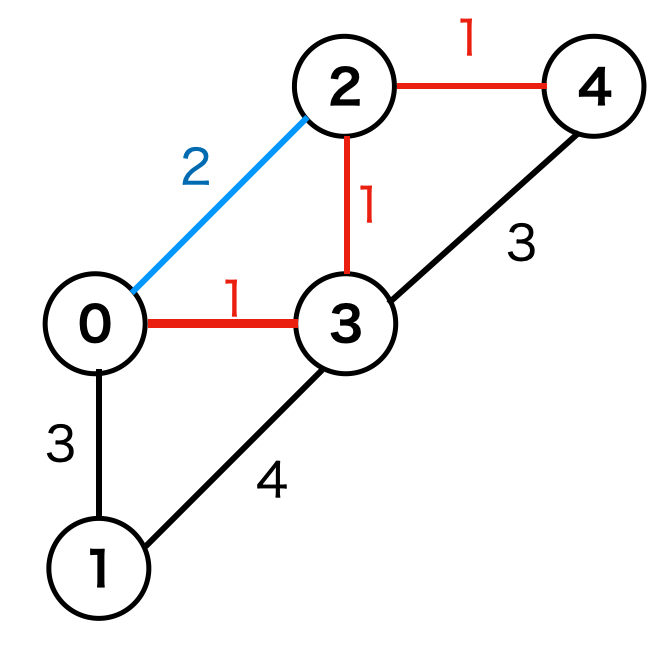
5番目の辺
(3, (0, 1)) に注目します。 頂点0と頂点1は異なるグループのため、辺をつなぎます。
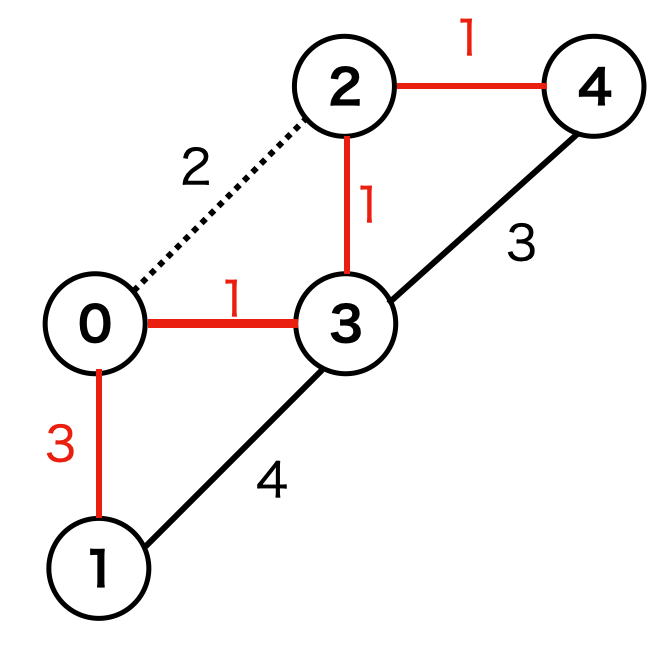
以上ですべての頂点を1つのグループ(木)にできたので、アルゴリズムは完了しました。( Edges の残りはすべて uf.isSame(u,v)=True となるため、答えに影響しません。)
最小全域木の答えは赤の辺の重みを足し合わせてわかります。今回は答えが 6 であることがわかりました。
まとめと参考
本記事ではクラスカル法に関して、pythonコードの実装と簡単なグラフでの実行の流れをまとめました。初学者の方(私も含めて)にもイメージしやすいよう、各辺に対するアルゴリズムの挙動を丁寧に取り上げました。
今回のコードは、 AOJ ALDS1_12_A で正解になることを確認しています。
また、クラスカル法の実装にはUnion-Find木の知識が重要です。私の過去の記事でもまとめているので、興味があればご覧ください。
さらに、最小全域木を求める他のアルゴリズムにプリム法というアルゴリズムも存在します。私の過去の記事でもまとめていますので、ご興味があればご覧ください。
本記事の執筆にあたって、以下の書籍を参考にしました。
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年




コメント