BIT(Binary Indexed Tree)をpythonで実装する

BIT(Binary Indexed Tree)は数列 $a_0, a_1,…,a_N$ に対して、以下の操作を $O(\mathrm{log} N)$ で実行できる二分木のデータ構造です。

$a_i$ に任意の数値 $x$ を加算
$\sum_{k=0}^i a_k $ を計算

また、このデータ構造は名前にもあるように、2進数のビット演算を用いてデータの管理を行います。この2進数の計算についても説明していきたいと思います。

BITの実装コード
BITの特徴
1. BITのイメージ図
2. 2進数を用いたインデックスの特定
BITでのadd関数の実行の流れ
BITでのsum関数の実行の流れ
使い方の例
まとめと参考

BITの実装コード

BITの実装コードを以下に記述します。

class BIT:

    #初期化
    def __init__(self, n):
        self.size=n
        self.tree = [0] * (n+1) #1-indexのリストで管理
    
    #加算
    def add(self, i,x):
        while i <= self.size:
            self.tree[i] += x
            i += i & -i       #LSBの計算
    #インデックス0からiまでの総和を計算
    def sum(self, i):
        total = 0
        while i >0:
            total += self.tree[i]
            i -= i & -i       #LSBの計算
        
        return total

BITの特徴

$N=8$ の場合を例にして、BITがどういうデータ構造なのか追っていきます。

BITの特徴として、以下の2点が挙げられます。

二分木構造のうち、右下の要素をあえて欠損させてメモリを削減
インデックスの特定に2進数計算を利用

BITのイメージ図

BITは数列 $a_1, a_2, …, a_8$ に対して、以下のような二分木を用いて管理します。

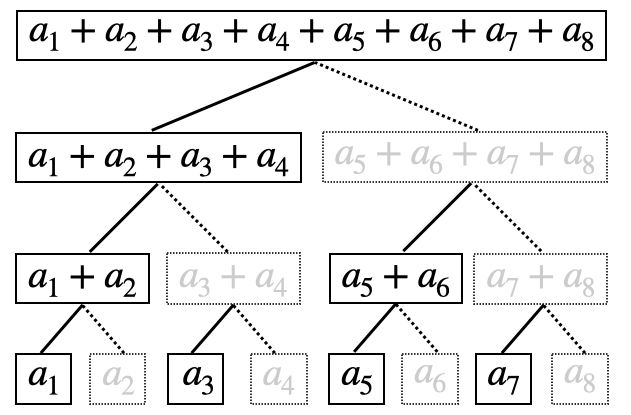
BITでは、上記の二分木のうち、黒実線で囲まれた値のみを管理します。各黒枠の右下にある点線枠の値はメモリに保持しません。

なぜなら、点線で囲まれた部分については、その左と上の要素を用いることで復元することができるからです。

例えば、 $a_2$ の値を知りたければ、その左の $a_1$ と上の $a_1+a_2$を用いて、

$$(a_1+a_2)\ -\ a_1$$

を計算すれば求められます。

2分木の要素全てを管理するには $2N-1$個の要素を保持する必要がありますが、この工夫によって、BITでは $N$ 個だけで済みます。

太線の枠で囲った要素は、以下のようにpythonのリストで管理されます。リストのインデックスと木の要素の末尾のインデックスが対応しています。

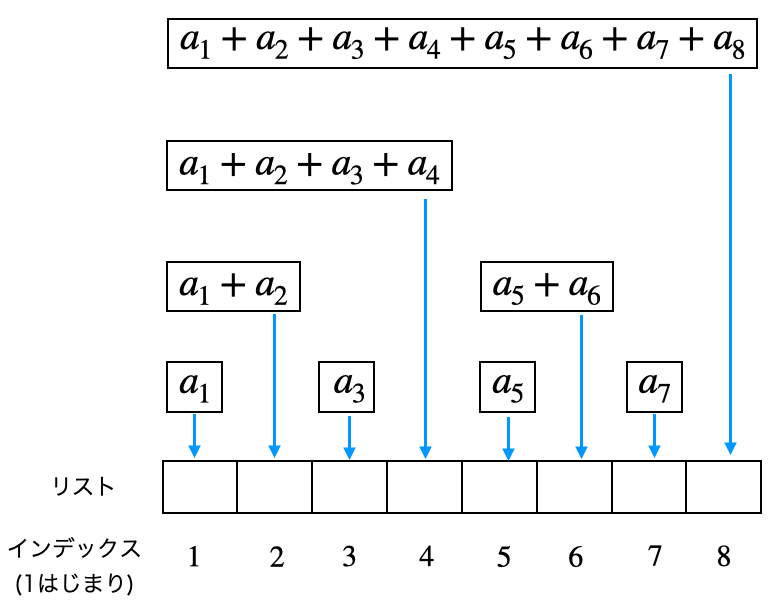
図2: BITをリストで管理する. リストのインデックスと木の要素の末尾のインデックスが対応しています。例えば、$a_1+a_2$の末尾のインデックスは2で、管理するリストのインデックスも2です。

2進数を用いたインデックスの特定

インデックスの計算に用いている負の数の2進数変換について述べます。この操作は『2の補数』と呼ばれています。今回はBITに必要な計算方法にのみ触れます。

負の数の2進数変換は、以下の一連の操作で実行できます。

数値を10進数から2進数に変換する
変換した2進数に対し、全桁のビットを反転する
反転したビットに2進数の1を追加する

例として、 $-4$ に上記の操作を実行してみます。

まず、4を2進数に変換すると $0100_{(2)}$ です。

次に、全桁のビットを反転(0->1, 1->0)すると、 $1011_{(2)}$です。

これに1を追加すると、 $1011_{(2)} + 0001_{(2)} = 1100_{(2)}$ となります。

以上で、 $-4 = 1100_{(2)}$ となることがわかりました。

この計算がコード上でどう振る舞うかは下の章で詳しくみていきます。

BITでのadd関数の実行の流れ

#BIT クラス
def add(self, i,x):
        while i <= self.size:
            self.tree[i] += x
            i += i & -i       #LSBの計算

例として $a_5$ に数値 $x$ を追加する場合を考えます。この場合、$a_5$ より上の要素 $a_5+a_6$, $a_1+…+a_8$にも $x$ を追加する必要があります。

リストでいうと、インデックスが5, 6, 8の要素に $x$ を追加する必要があります。これらの要素に足されていく過程を見ていきます。

$i=5$の場合

赤丸の部分に $x$ が足されます。

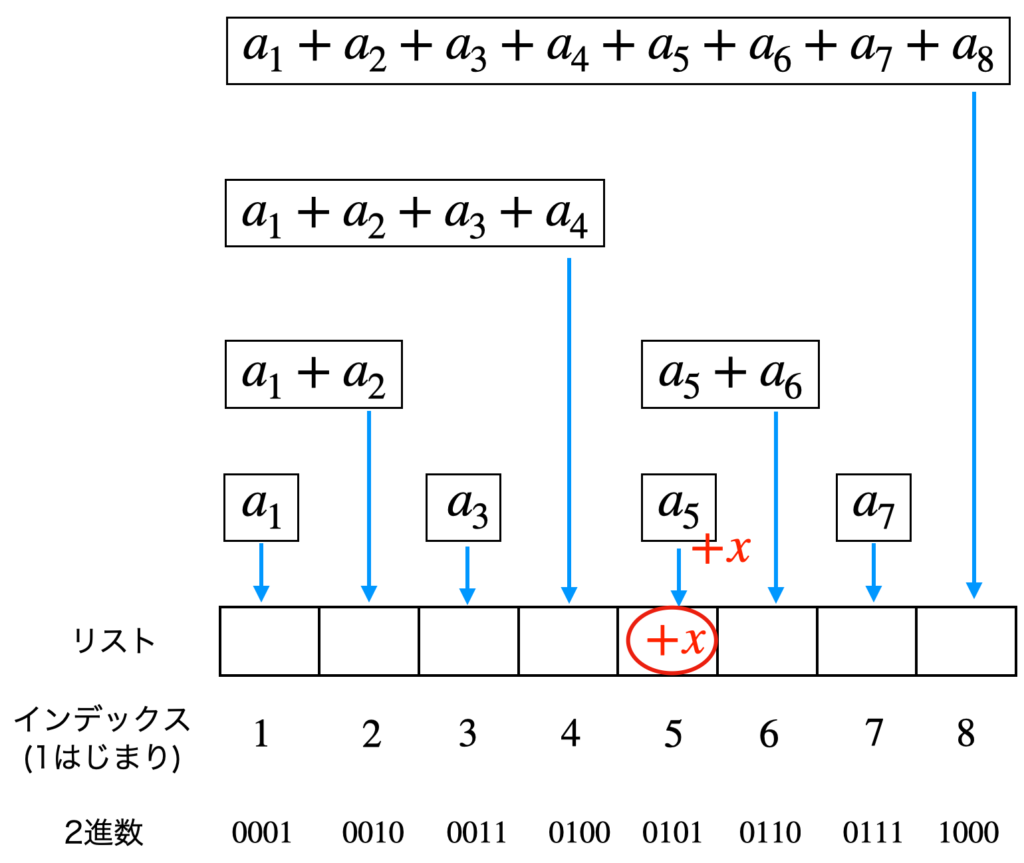
その後、次のインデックスに移ります。インデックス計算は以下の通りです。

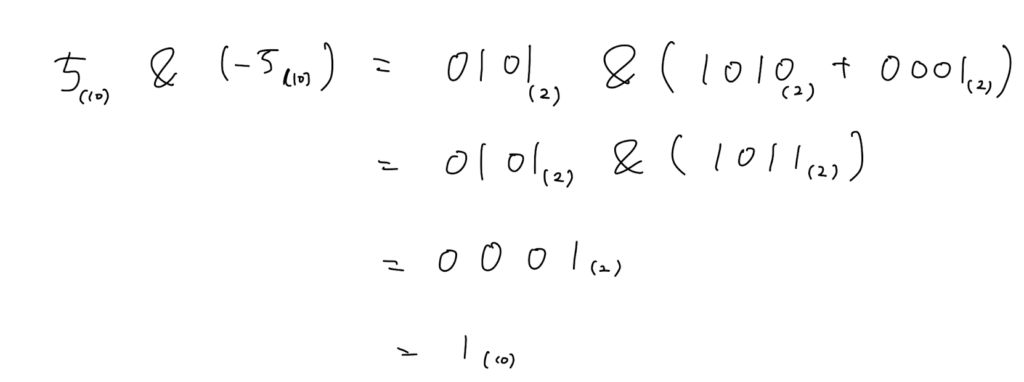
式1: 次のインデックスを求める計算. 1行目は10進数から2進数に変換します。変換の際、-5は2の補数を利用して変換しています。2,3行目ではand計算をしています。

この式の計算結果より、次のインデックスは $5+1=6$ とわかりました。

$i=6$の場合

この場合も流れは $i=5$ の場合と同様で、リストの赤丸の要素に $x$ が追加されます。

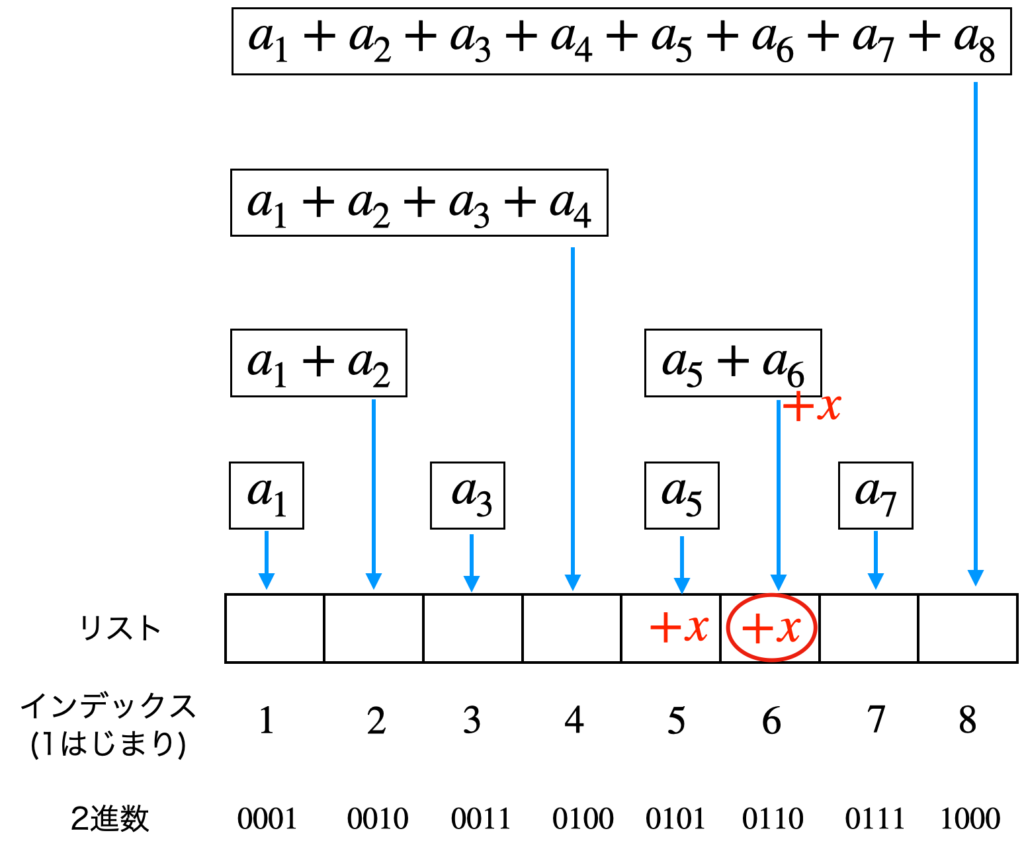
次のインデックスは、以下の計算から $i=6+2=8$ とわかる。

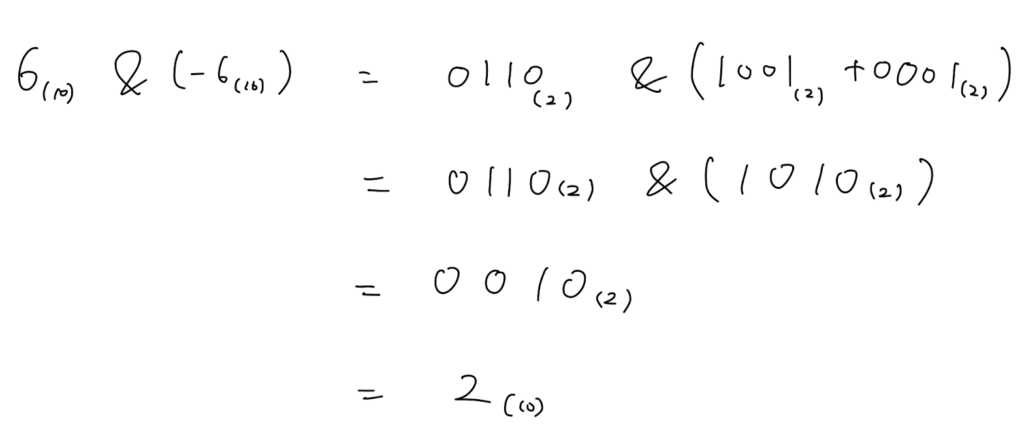
$i=8$の場合

リストの赤丸の要素に $x$ が追加されます。

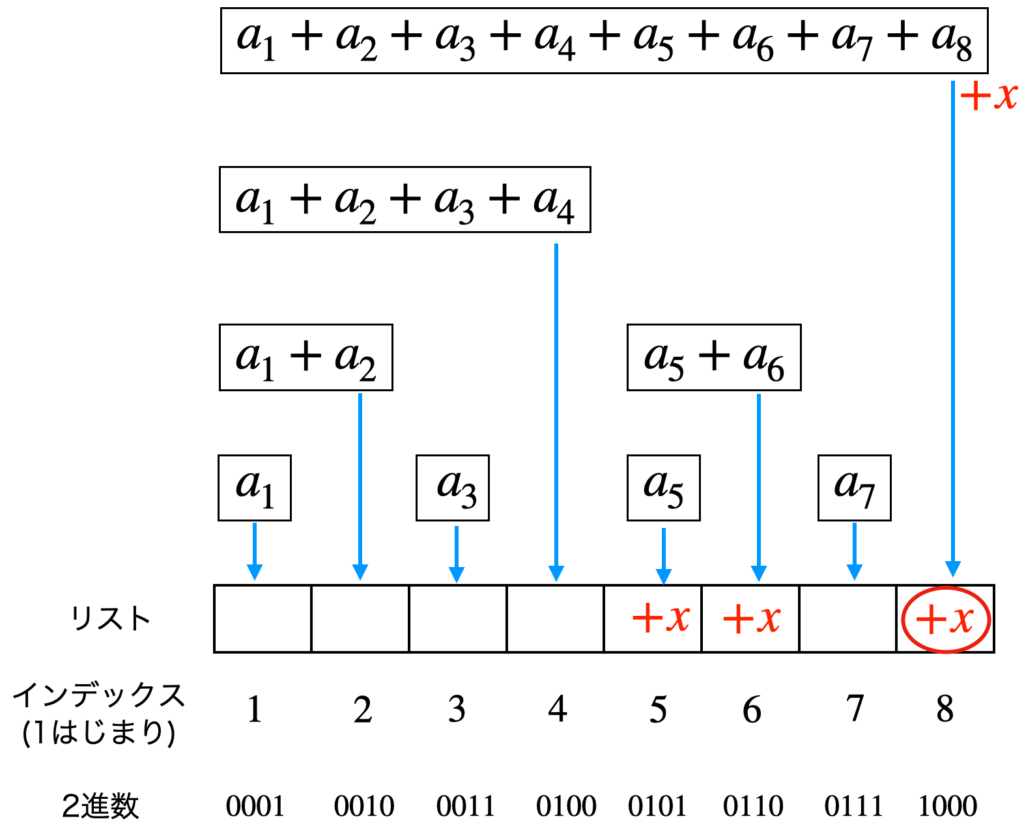
$i=8$ より大きいインデックスは存在しないため、add関数は終了します。

BITでのsum関数の実行の流れ

def sum(self, i):
        total = 0
        while i >0:
            total += self.tree[i]
            i -= i & -i       #LSBの計算

例として、$i=7$ の場合を考えます。得られる結果は、$a_1+a_2+…+a_7$ の値となります。

$i=7$の場合

$a_7$ の値が変数 total に追加されます。

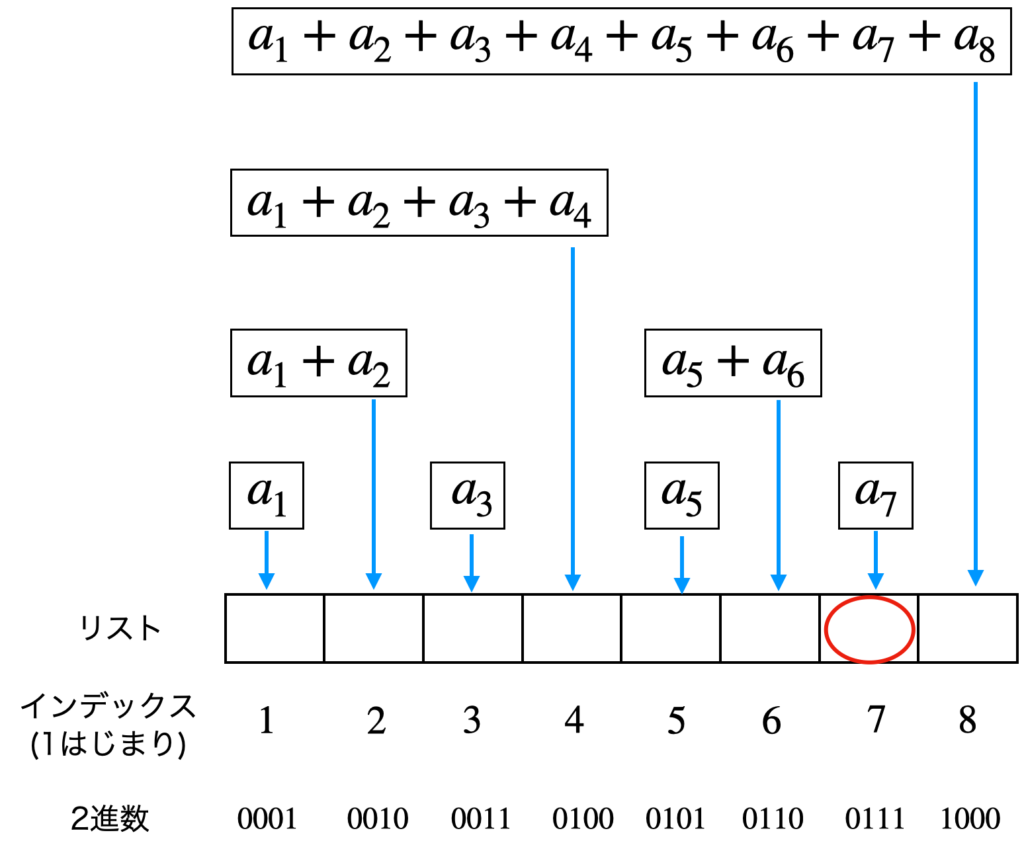
その後、次のインデックスを計算します。add関数の場合と同様に、2進数を用いて計算します。

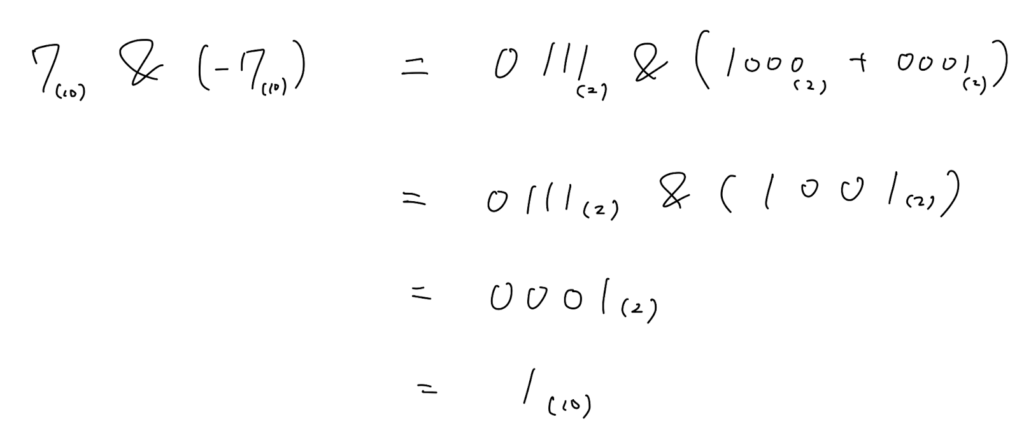
計算の結果、$i=7-1=6$ に移動します。

$i=6$の場合

変数 total に、インデックス $i=6$ の要素 $a_5+a_6$ を追加します。

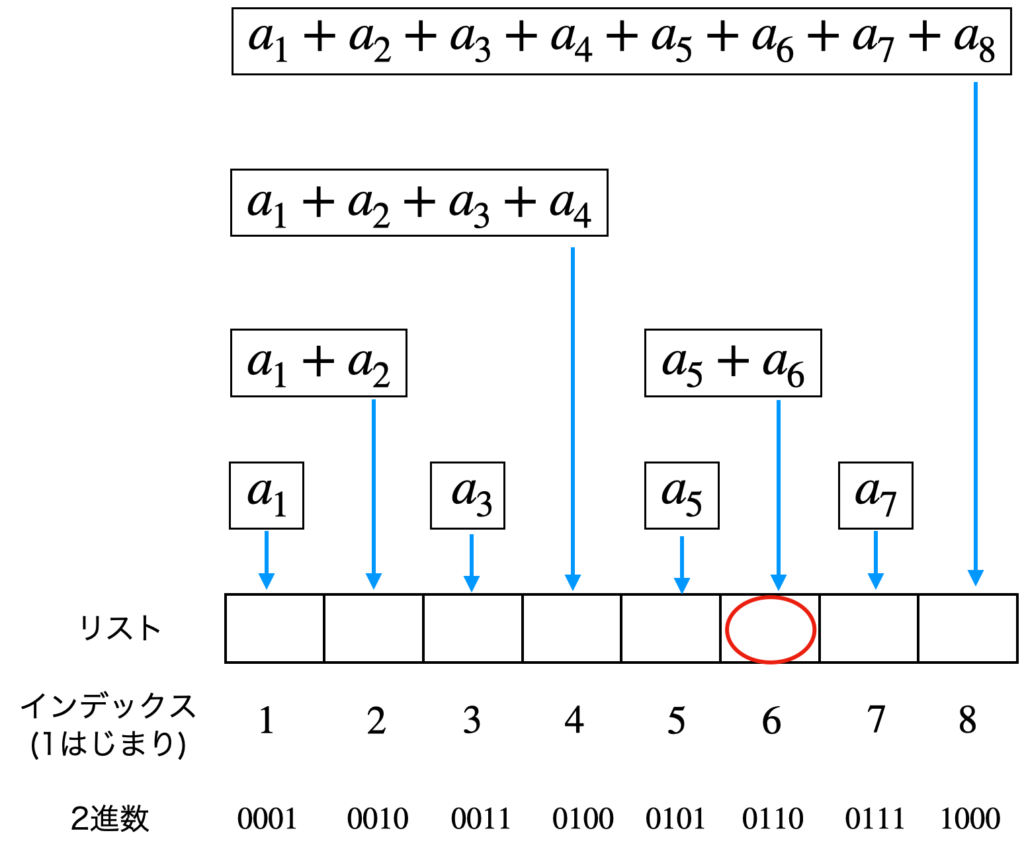
次のインデックスは、式2の結果を用いて $i=6-2=4$ となる。

$i=4$の場合

変数 total に、インデックス $i=4$ の要素 $a_1+a_2+a_3+a_4$ を追加します。

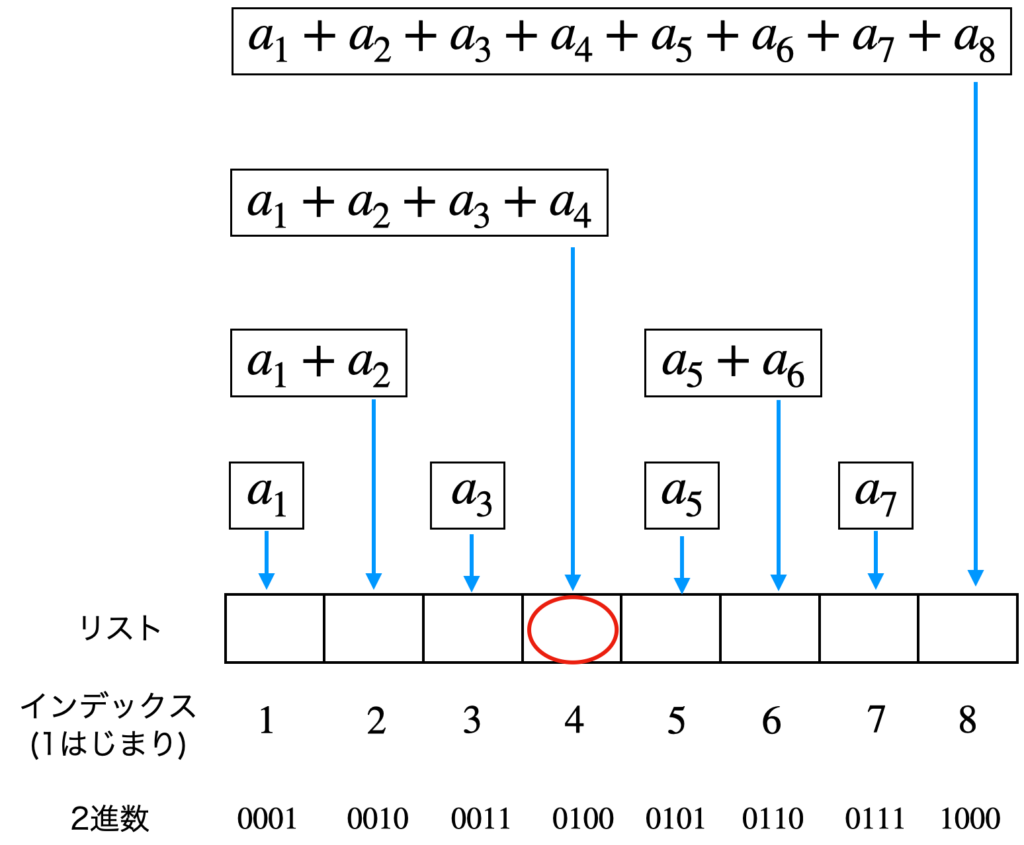
次のインデックスは、以下の計算から、

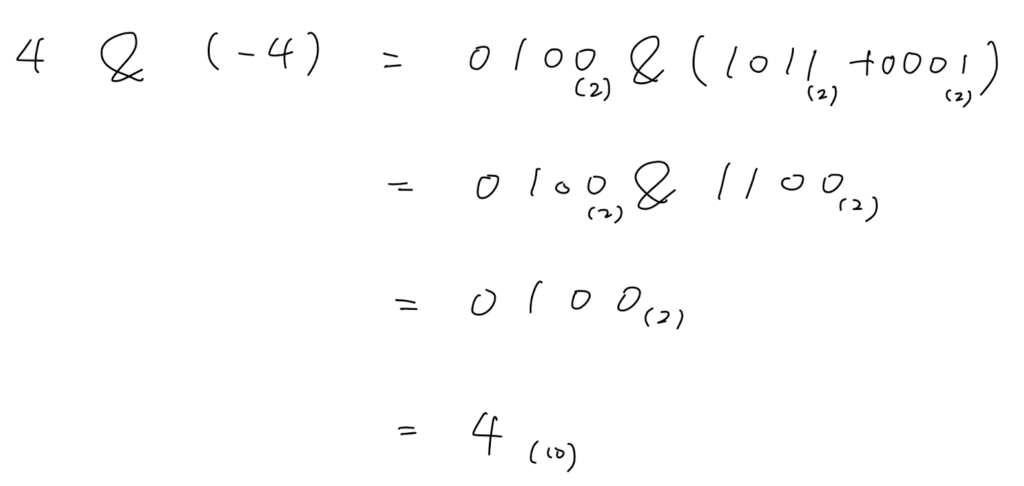
$i=4-4=0$ となり終了します。

変数 total に足された値をみると、

$$ total = (a_7) + (a_5+a_6) + (a_1+a_2+a_3+a_4)$$

となっており、確かに$a_1+…+a_7$が計算できていることがわかります。

使い方の例

最後に、A = [1,2,3,4,5,6,7,8] をBIT化する方法について述べたいと思います。

class BIT:
    #...略...

A = [1,2,3,4,5,6,7,8] #入力リスト
N = len(A)
bit = BIT(N)          #BITを呼び出す
for i, a in enumerate(A):
    bit.add(i+1, a)   #Aの各項目をbitにaddしていくことで、AをBinaryIndexedTreeで管理できる

#bit=[0, 1, 3, 3, 10, 5, 11, 7, 36]

for文でAの各要素をBITに追加していくことで、単なるリストをBITで管理できるようになります。

まとめと参考

BITという特殊な木構造についてpythonのコードと、具体的な計算の流れについてまとめました。

最後に、BITの特徴として

二分木構造のうち、右下の要素をあえて欠損させてメモリを削減
インデックスの特定にLSB(Least Significant Bit) という2進数計算を利用

が挙げられ、値の追加・区間和を $O(\mathrm{log N})$ で計算できます。

本記事執筆にあたり、以下のリンクを参考にしました。

Binary Indexed Tree（Fenwick Tree）: BIT(別名 Fenwick Tree) が詳しく紹介されていました。

Binary Indexed Tree のスライド : アルゴリズムの流れなどわかりやすかったです。

2の補数を分かりやすく解説 : インデックス計算に用いる2の補数に関する記事です。

また、以下の書籍にもBITが詳しく説明されており、参考になりました。

『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、岩田陽一、北川宜稔, マイナビbooks, 2012年