グラフの表現方法について解説します。注意として、本記事の行列などはすべては0始まりで表現します。
グラフについて
グラフは物や状態の結びつき方を表現した抽象的なデータ型で、ノード(頂点)群とそれらをつなぐエッジ(辺)で構成されています。
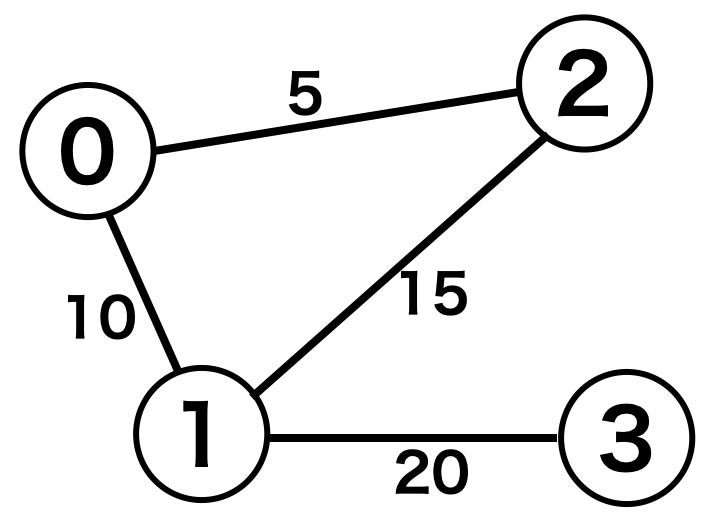
場合によっては各辺にコスト(重み)が書かれています。これは距離や移動時間などを表現しています。
隣接行列
これは頂点数を$N$個としたとき、$N \times N$ の行列で繋がっているか否かを表現したものです。$i$ 行 $j$ 列目が1の場合は頂点 $i, j$ は繋がっており、0の場合は頂点 $i, j$ は繋がっていないという定義です。
隣接行列は表で書くとわかりやすいと思います。

例えば図2の頂点0と頂点2を見ると辺で繋がっています。表1でこの部分に相当するのは0行2列目、もしくは2行0列目です。これらを見ると1となっていてつながりを表現できています。
隣接行列ではノード間のコストは管理できないことに注意が必要です。
距離行列
隣接行列と同じく $N \times N$ の行列で表現されます。$i$ 行 $j$ 列目の要素は頂点 $i, j$ 間のコストを表しています。
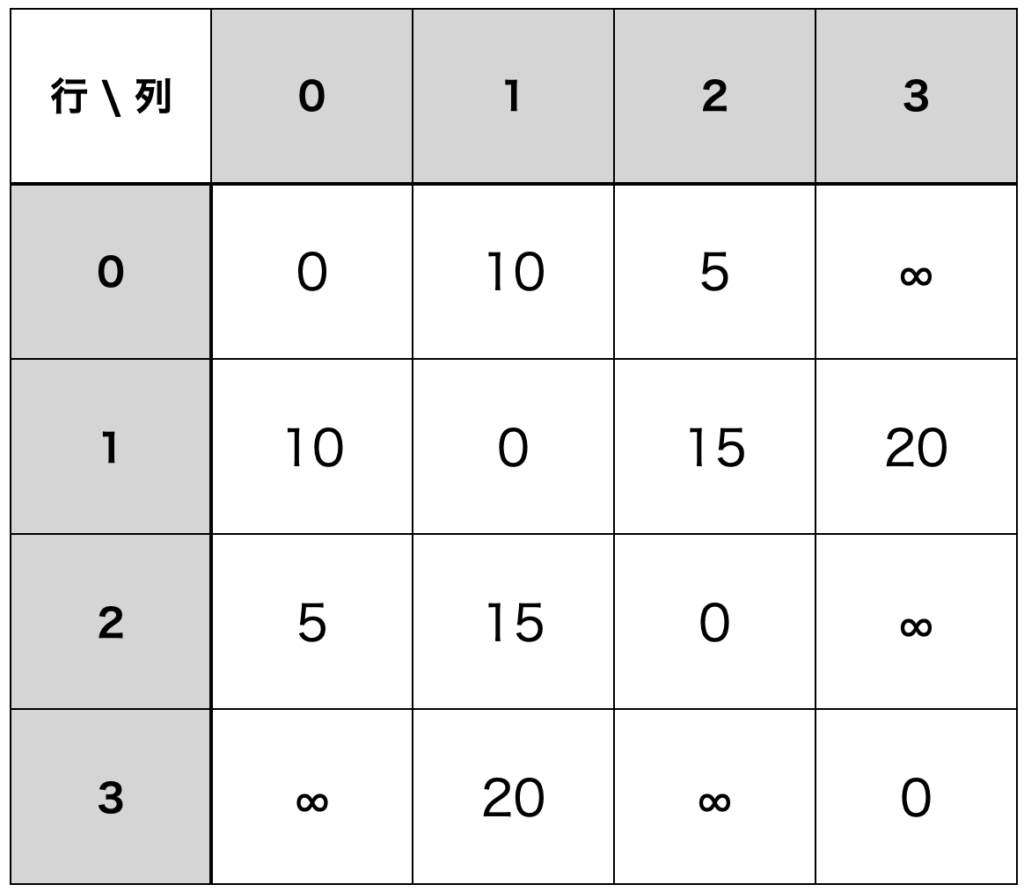
例えば図2の頂点0と頂点2を見るとコスト5で繋がっています。表2で相当する0行2列目、もしくは2行0列目を見ると、5となっています。また、0行3列のように繋がっていない頂点同士は $\inf$ とします。
隣接リスト
上記の2つの行列は $O(N^2)$ のメモリを消費するデメリットを持っています。これを解決するためにリストでグラフを表現したものが隣接リストです。
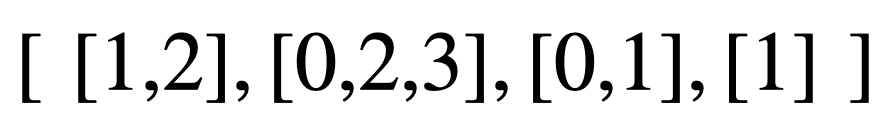
行列では繫がってない頂点も0や $\inf$ で管理する一方、隣接リストでは繫がっていない辺を管理しない設計となっています。そのため、行列よりも効率的です。
辺の本数を $N$ 本とした場合、メモリの消費はせいぜい $O(N)$であり、行列を用いるよりも効率的です。
隣接行列を隣接リストで表現
隣接行列を隣接リストで表現すると以下のようになります。
隣接リストでは、$i$番目のリストには頂点 $i$ と繋がっている頂点番号が管理されます。
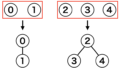
例えば、0番目の $[1,2]$ は、 頂点0が頂点1と 頂点2 とが辺で繋がっているということを表しています。
距離行列を隣接リストで表現
以下の図のように距離行列を隣接リストで表現できます。
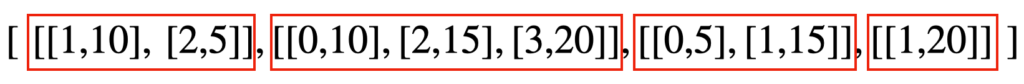
赤い枠がそれぞれ0, 1, …, 3番目の頂点が繋がっている辺を管理しています。そして、各赤枠内の各リストは $[頂点, コスト]$ という意味を表しています。
例えば、先頭(0番目)の赤枠を見ると、頂点0と頂点1がコスト10で繋がり、さらに頂点0と頂点2がコスト5で繫がっていることが読み取れます。
まとめと参考
グラフの表現方法についてまとめました。隣接行列・距離行列はわかりやすい一方、メモリ消費が $O(N^2)$ で非効率的です。対して、隣接グラフは少し難しめですが、メモリ消費が $O(N)$ で効率的です。
慣れれば隣接リストの方が便利だと思います。
本記事では以下の書籍を参考にしました。
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビ出版, 2012年

コメント