競技プログラミングを勉強している中で、二次元のグリッドを使った問題と度々出会います。解いた問題の備忘録も兼ねて、問題とその解法についてまとめておきます。
二次元グリッドの問題例
有名なものでは、グリッドの最短経路の数え上げが挙げられます。高校数学の典型問題として有名なものです。
この問題については以下のサイトで複数の解法(動的計画法、メモ化再帰、重複順列)について解説しています。ご参照ください。
AtCoder Beginner Contest87 C
2×N のマス目があります。上から i 行目、左から j 列目 (1≤i≤2, 1≤j≤N) のマスをマス (i,j) と表すことにします。
あなたははじめ、左上のマス (1,1) にいます。 あなたは、右方向または下方向への移動を繰り返し、右下のマス (2,N) に移動しようとしています。
マス (i,j) には $A_{i,j}$ 個のアメが置かれています。 あなたは移動中に通ったマスに置いてあるアメをすべて回収します。 左上および右下のマスにもアメが置かれており、あなたはこれらのマスに置かれているアメも回収します。
移動方法をうまく選んだとき、最大で何個のアメを回収できるでしょうか。
AtCoder Beginner Contest87 C-Candies
解法1: 重複順列をすべて確認する
$N\leq 100$であるため、全経路 ${}_{100} \mathrm{C}_2 <10^4$ を探索することができます。
from collections import deque
N = int(input())
A = []
for _ in range(2):
a = list(map(int, input().split()))
A.append(a)
#全通りを試すことが可能
#0=右, 1=下へ移動
ans = 0
for i in range(N):
#先頭からi番目を1にする
route = [0]*N #0=右に移動、1=下に移動
route[i] = 1
row,col = 0,0
tmp = 0
q = deque()
q.append([row,col])
for j in range(N):
tmp += A[row][col]
if route[j] == 0:
col += 1
else:
row += 1
tmp += A[-1][-1]
ans = max(ans, tmp)
print(ans)- route は0か1で構成されるリストで、0なら右移動、1なら下移動を意味します。0が$N-1$個,1が1個の重複順列として解釈できます。
- 最初のfor文では、どの地点で下に移動するかを決めます。
- 2個目のfor文では、スタートからゴールまで経路をたどってアメを集めます。
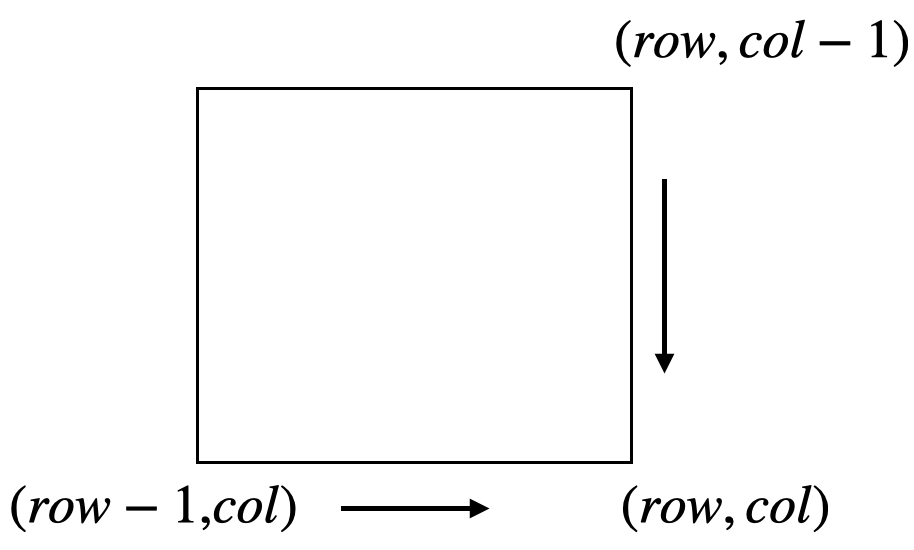
解法2: 動的計画法
N = int(input())
A = []
for _ in range(2):
a = list(map(int, input().split()))
A.append(a)
#動的計画法
dp = [[0]*N for _ in range(2)]
dp[0][0] = A[0][0]
for row in range(2):
for col in range(N):
if row == 0 and col == 0:
continue
#一行目にいる場合
if row == 0:
dp[row][col] = dp[row][col-1] + A[0][col]
#一列目にいる場合
elif col == 0:
dp[1][0] = dp[0][0] + A[1][0]
else:
dp[row][col] = max(dp[row-1][col],dp[row][col-1])+A[row][col]
print(dp[1][-1])基本的なアイデアは以下のイラストの通りです。
AtCoder Beginner Contest 293 C
H 行 W 列のマス目があります。 1≤i≤H かつ 1≤j≤W を満たす 2 つの整数 $i,j$ について、 上から i 行目、左から j 列目のマス(以下、(i,j) と表す)には、整数 A_{i,j} が書かれています。
いま、高橋君は (1,1) にいます。 これから高橋君は「いまいるマスから右または下に隣接するマスに移動する」ことを繰り返して、(H,W) まで移動します。 ただし、その過程でマス目の外部に移動することは出来ません。
その結果、高橋君が通ったマス(始点 (1,1) と終点 $(H,W)$ を含む)に書かれた整数がすべて異なるとき、高橋君は嬉しくなります。 高橋君の移動経路として考えられるもののうち、高橋君が嬉しくなるものの個数を出力してください。
AtCoder Beginner Contest 293 C-Make Takahashi Happy
$H,W \leq10 $ であるため、全経路 $\frac{(H+W-2)!}{(H-1)!(W-1)!}通り$ を探索することが可能です。
from itertools import combinations
H, W = map(int, input().split())
A = []
for _ in range(H):
row = list(map(int, input().split()))
A.append(row)
ans = 0
for cmb in combinations(range(H+W-2), H-1):
#0=右移動, 1=下移動
route = [0] * (H+W-2)
#下方向にいつ行くか
for i in cmb:
route[i] = 1
h,w = 0,0
tmp = set()
#各経路を辿ってみる
for i in range(H+W-2):
tmp.add(A[h][w])
#右へ移動
if route[i] == 0:
w += 1
#下へ移動
else:
h += 1
tmp.add(A[-1][-1])
if len(tmp) == H+W-1:
ans += 1
print(ans)まとめ
グリッドを使った問題をいくつか取り上げて、解法をまとめました。
何か参考になれば幸いです。



