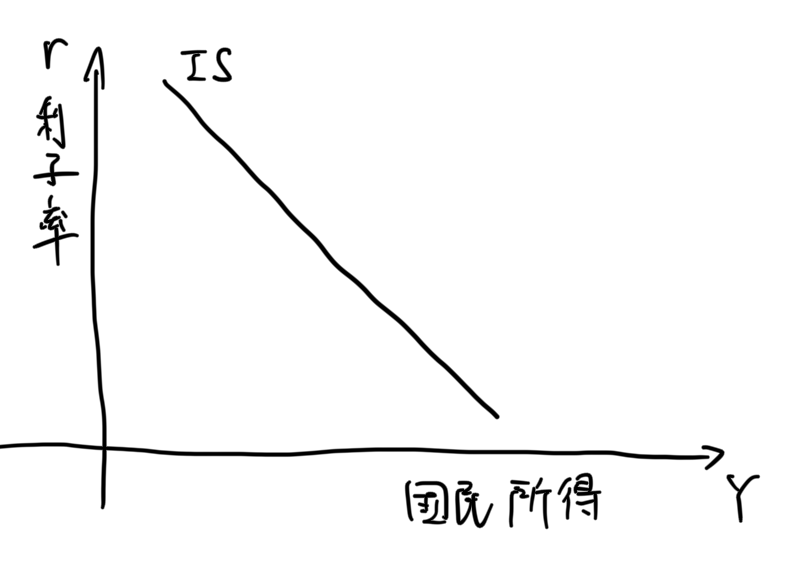
投資(Investment)と貯蓄(Savings)が均衡している状況での国民所得Yと利子率rの曲線として定義される。この曲線の導出法について簡単にまとめる
前提:家計+生産者+金融機関の関係
IS曲線を考えるにあたって、登場人物は家計・生産者・金融機関の3人になります。
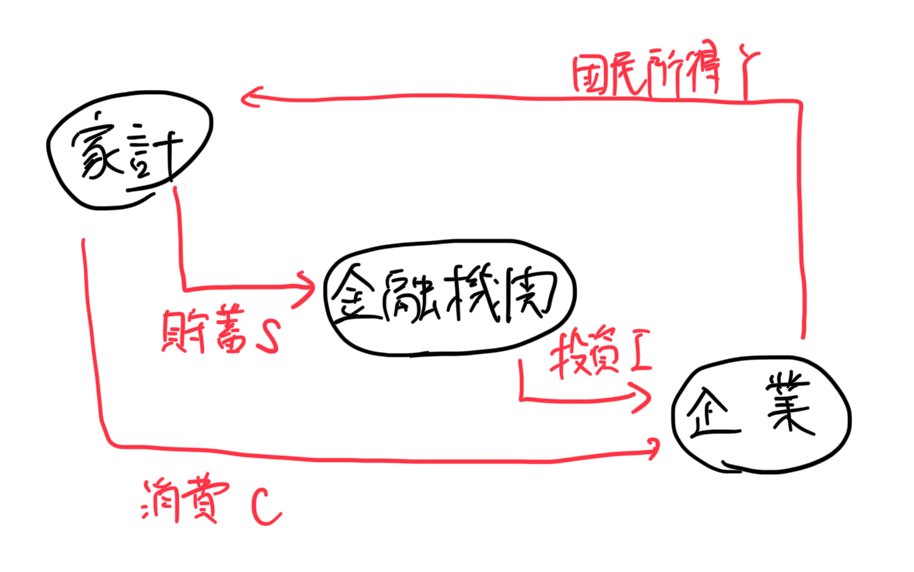
この3者間の関係を式に表すと、
$Y=C+I$
と書けます。
また、この図を消費者目線で見れば、
$S=Y-C$
と書くこともできます。受け取った給与$Y$のうち、$C$を消費したら $Y-S$だけ貯蓄に回すことができるという意味で、とても当たり前のことを表しています。
この2式からYを代入すると
$S = (C+I)-C → I=S$
と書くことができます。これが冒頭で述べた、投資(Investment)と貯蓄(Savings)の均衡になります。
IS曲線の導出
次は (1)式について、利子率との関係性を見ていきます。
C(消費)についてみると、所得が多いほど消費金額も多くなることは直感に反しないと思います。
$C \propto Y \rightarrow C = cY+C_0$
ただし、c=限界消費性向($0<c<1$)と呼びます。
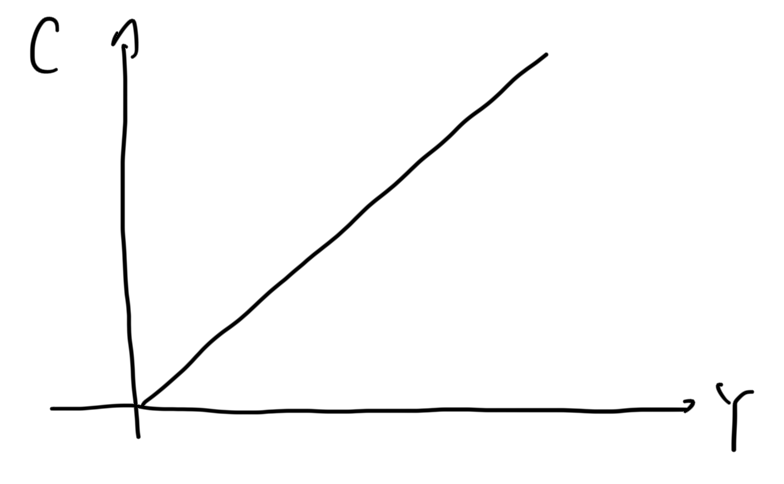
I(投資)については、逆の動きをします。
$I \propto -r \rightarrow I = -ir +I_0$
ただし、$i$=投資の利子感度, $r$=利子率です。

・利子率がdown → 返すお金が小さくなるため、借りやすくなる → 企業が投資金額がup
・利子率がup → 返すお金が増えて借りにくくなる → 企業の投資金額がdown
の流れになります。
以上の式を(1)へ代入すると、
$Y = cY+C_0 + -ir + I_0$
式変形すると、
$r = -\frac{1-c}{i}Y + \frac{C_0+I_0}{i}$
以上より、右下がりのIS曲線が導出できました。
IS曲線の解釈
このIS曲線と最初の3者間の関係図を使って、IS曲線のシフトについて考えてみます。
利子率と所得の関係
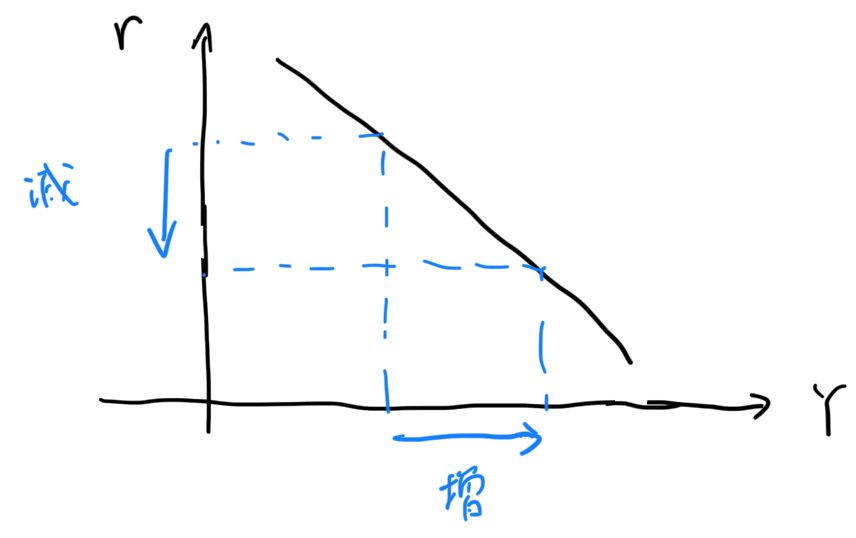
$r \propto -Y$
が成り立つ( $0<c<1$ のため、傾きは正になることはない)ため、利子が上がれば所得は小さくなります。その逆も然りで、利子が下がれば所得は大きくなります。
利子率が国民所得に影響する理由は、最初の3者間の図で理解できます。
・利子率がdown → 返すお金が小さくなるため、借りやすくなる → 企業が投資金額がup → 生み出す利潤がup → 国民所得がup
・利子率がup → 返すお金が増えて借りにくくなる → 企業の投資金額がdown → 生み出せる利潤が減少 → 国民所得がdown
右シフトについて
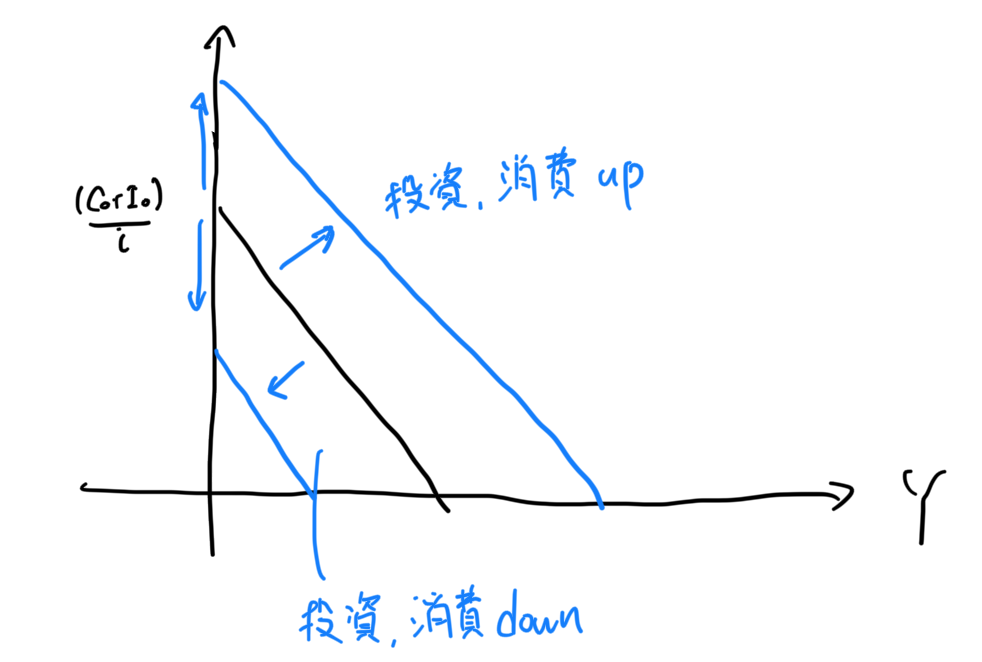
IS曲線が右にシフトする場合を考えてみます。右にシフトするということは、切片が大きくなることを意味します。こう考えると、
・消費、投資が増える
ことで実現されることと解釈できます。
逆に、左のシフトは切片が小さくなることなので、
・消費、投資が減る
と解釈できます。
まとめ
IS曲線の導出と解釈について述べました。前提にある家計・企業・金融企業の関係図が頭にあれば自分で導出ができるようになり、ただ暗記するより理解しやすくなると思います。