1種類の財のみを生産する仮定のもとで、生産にかかる費用関数について考える。また、生産関数の損益分岐点と操業停止点についてまとめます。
本記事でやること
- 費用関数について(可変費用+固定費用)
- 損益分岐点=平均費用関数と限界費用関数の交点になる理由
- 操業停止点=平均可変費用関数と限界費用関数の交点になる理由
準備:平均費用関数・限界費用関数・平均可変費用関数
損益分岐点・操業停止点の理解に必要な3つのグラフについて整理します。
平均費用関数
平均費用は以下の式で定義されます。財1単位あたりの生産コストの意味を持ちます。この関数は一般的に逆S字形状になります。
平均費用(Average Cost, AC) = 総費用(Total Cost)/ 生産量(Q)この式を図形的に表現すると、費用関数上の点と原点を結ぶ直線の傾きとして理解することができます。
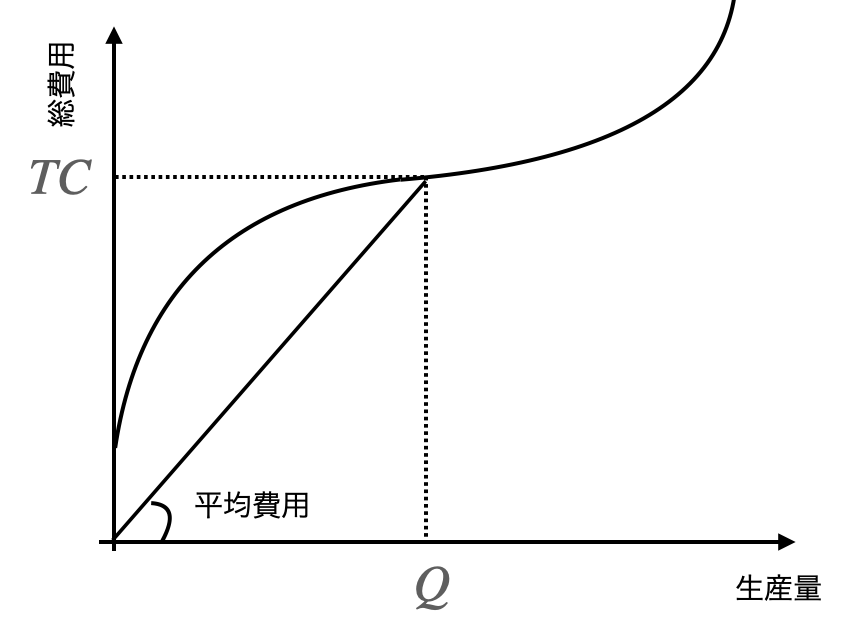
この値を費用関数上全て集めてプロットしたものが平均費用関数です。
平均可変費用関数
平均可変費用は以下の式で定義されます。
平均費用(Average Variable Cost, AVC) = 可変費用(Variable Cost)/ 生産量(Q)この式を図形的に表現すると、可変費用関数の切片とを結ぶ直線の傾きとして理解することができます。(総関数=固定費用+変動費用となります。)
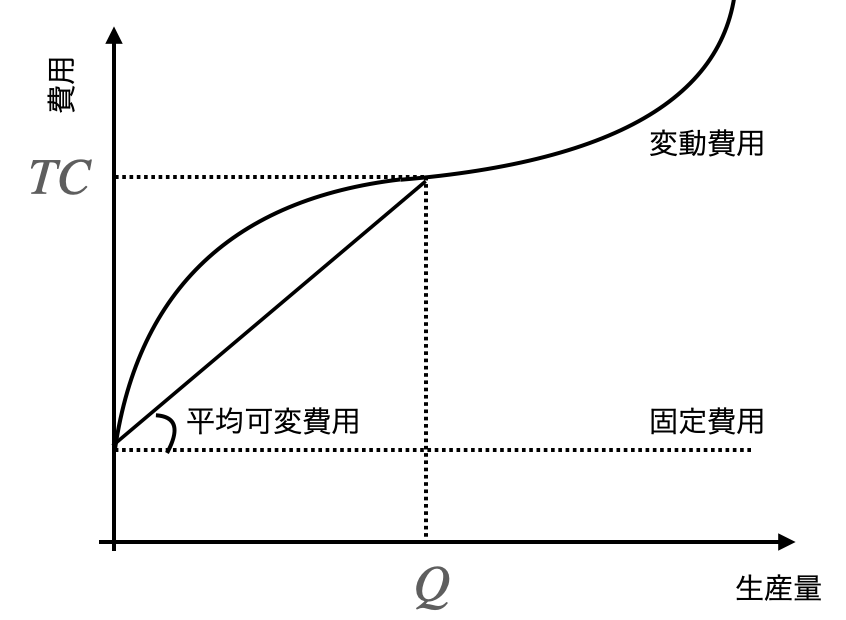
総費用関数と違って原点始まりではなく切片始まりであることに注意です。
限界費用関数
限界費用は以下の式で定義されます。費用関数の微分であり、その点から1単位生産を増やした際に追加でかかる費用の意味を持ちます。
限界費用(Marginal Cost, MC) = Δ費用関数/Δ生産量この式を図形的に表現すると、以下のようにある点での関数の傾きとして表現されます。
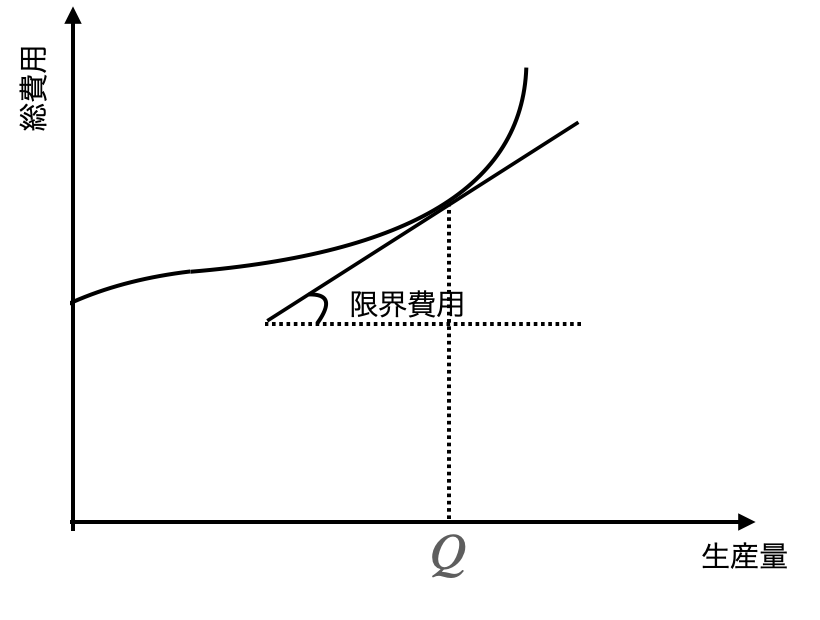
この値を費用関数上全て集めてプロットしたものが限界費用関数です。
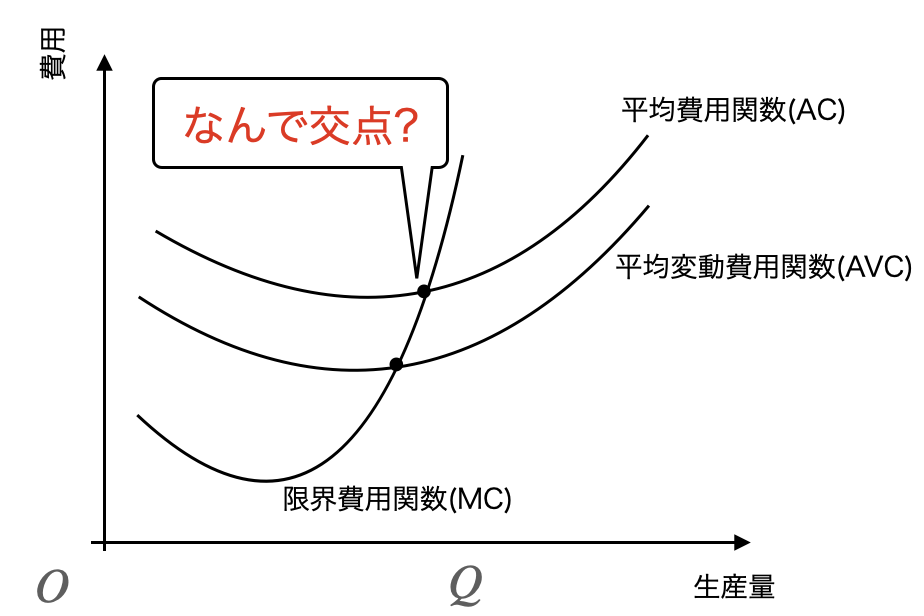
なぜ損益分岐点はACとMCの交点になるか
上で定義した平均費用関数(AC)と限界費用関数(MC)の交点が損益分岐点となります。
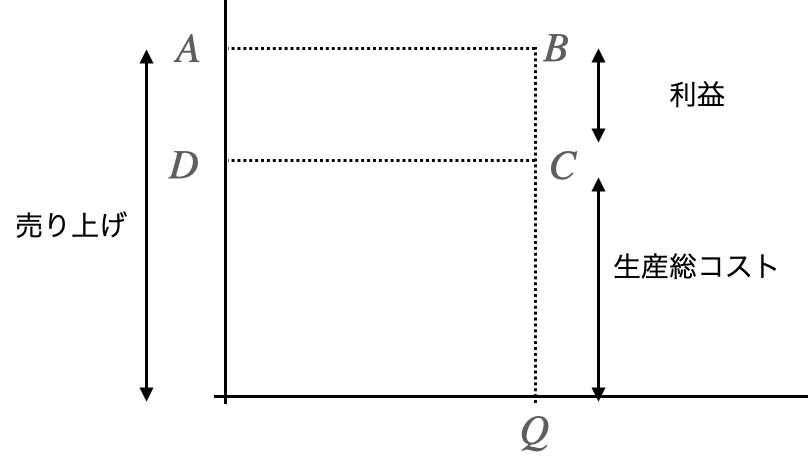
ある生産量Qの売り上げは長方形の面積ABQOで表現することができます。言い換えれば、限界費用関数で利益を求めることができます。
対して、その生産量を生産するのにかかるコストは長方形DCQOで表現することができます。(定義式から平均費用に生産量をかければ総費用になります。)
企業が得られる純利益は売り上げから生産にかかる総費用を引くことで求められます。
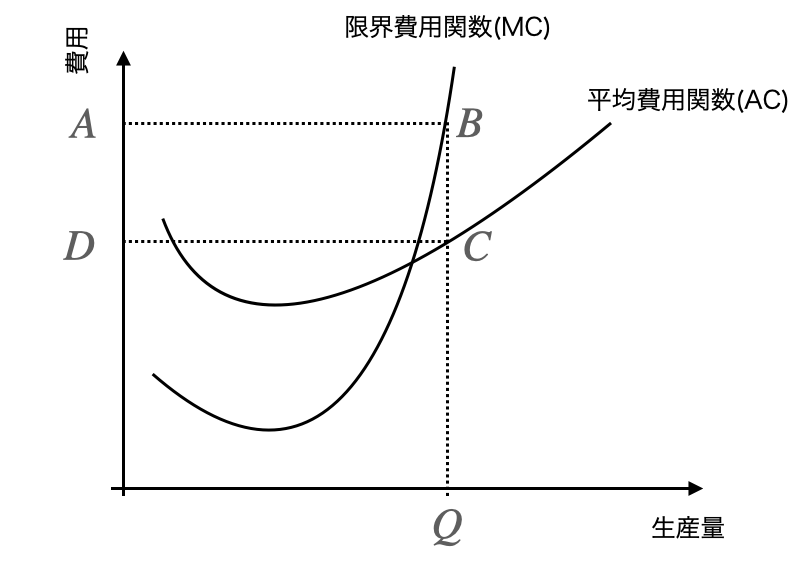
図形的に言えば、長方形ABCDの面積が企業が受け取れる純利益ということになります。
ということは、高さBC=0になれば、その企業の利益は0になることを意味します。
BC=0になるのは、MCとACの交点であり、この点のことを特別に損益分岐点と呼んでいるです。
なぜ操業停止点はAVCとMCの交点になるのか
生産量をQとした際、ACとAVCの差は固定費用の分を意味します。
図形的に言えば、AVCより上のABCDの部分は固定費用の回収に充てることができ、企業は生産をせざるを得ない状態といえます。
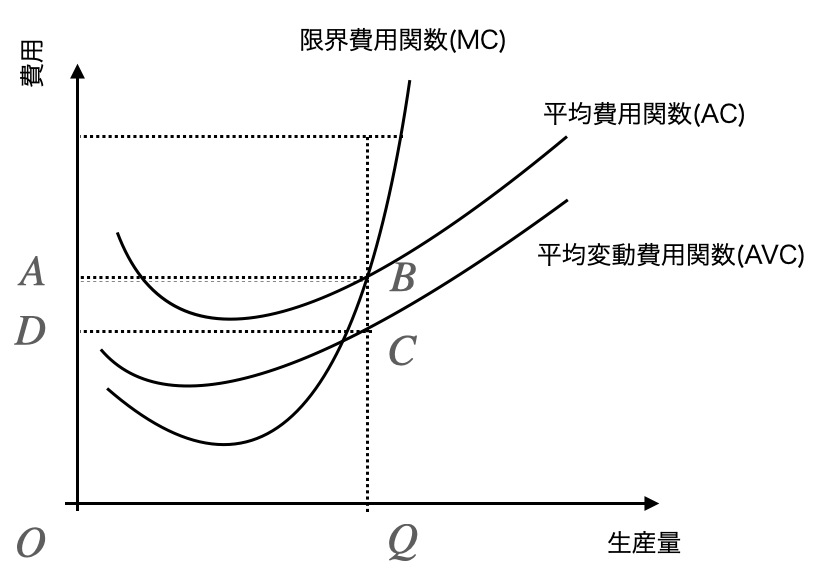
この高さが0になると、固定費用の回収に充てられる分が0となります。さらにAVCよりも下になると変動費用の分すら回収できないため赤字を出し続けることを意味します。
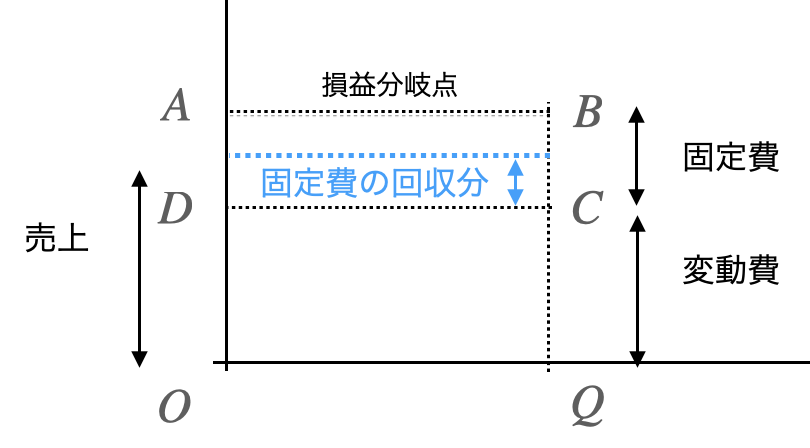
しかし、DCより下になると変動費すら賄えない。
そのため、AVCとMCの交点は赤字になる手前の状態として理解でき、ここを操業停止点と定義します。
まとめ
損益分岐点と操業停止点について解説しました。文字だけ聞いてもあまりイメージが湧かないですが、図形と一緒に考えるとだいぶわかりやすくなると思います。