k-means法(k平均法)を平たく言えば、データ間の距離の近さを基準に $k$ 個のクラスタ(クラス、まとまり)に分類する手法です。
教師なし学習という手法に分類されており、データ点の座標がわかっていれば使うことができます。そのため、データがどのクラスに分類されているかわかっている必要はありません。
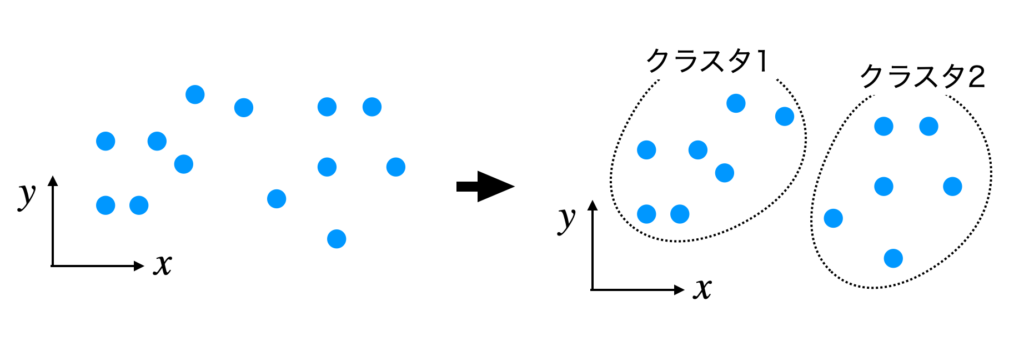
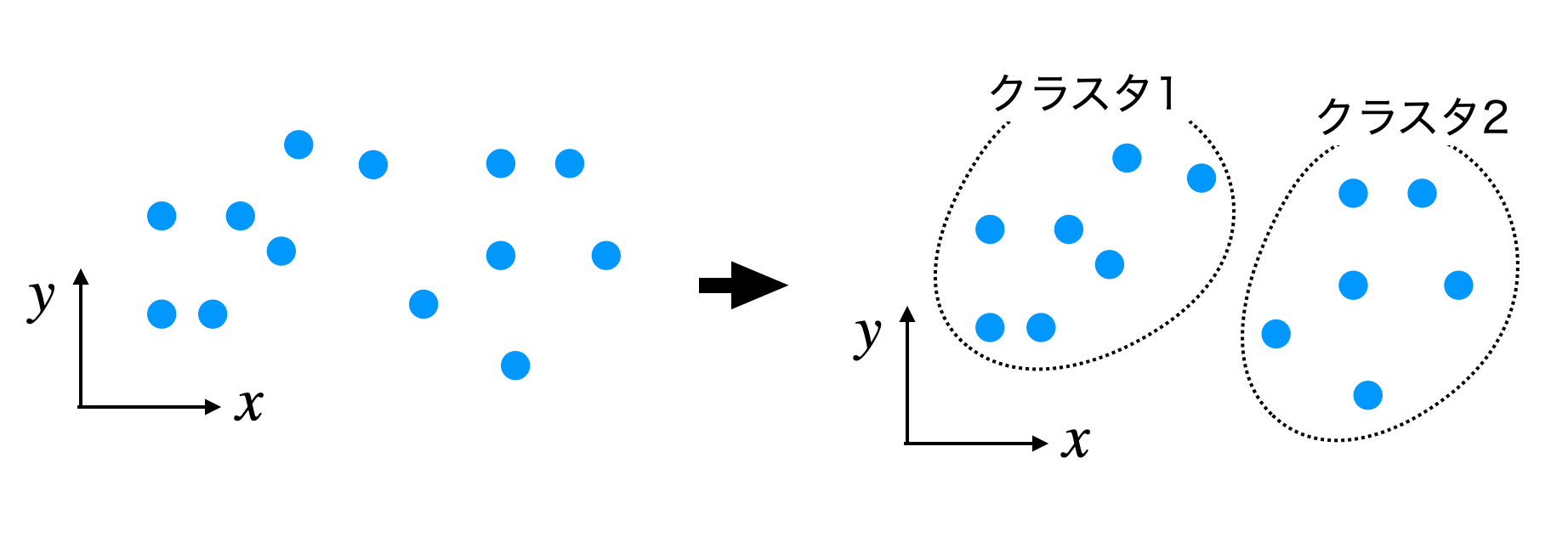
例として以下のように2次元空間に青のデータ点がある場合、kmeans法をk=2で実行すると、点線で囲まれたように2つのクラスに分割されます。
アルゴリズムの流れ
- データを $k$ 個のクラスにランダムに分割する
- 分割後のデータ点を用いて、各クラスの重心の初期値を計算する
- 各データ点を一番近い重心のクラスに更新する
- 更新後のデータ点を用いて重心の座標を計算し直す
- 3., 4. のプロセスを”条件”を満たすまで繰り返す
ここでいう『条件』とは、重心の移動がなくなる、もしくは規定のイテレーション回数まで繰り返すのどちらかになります。
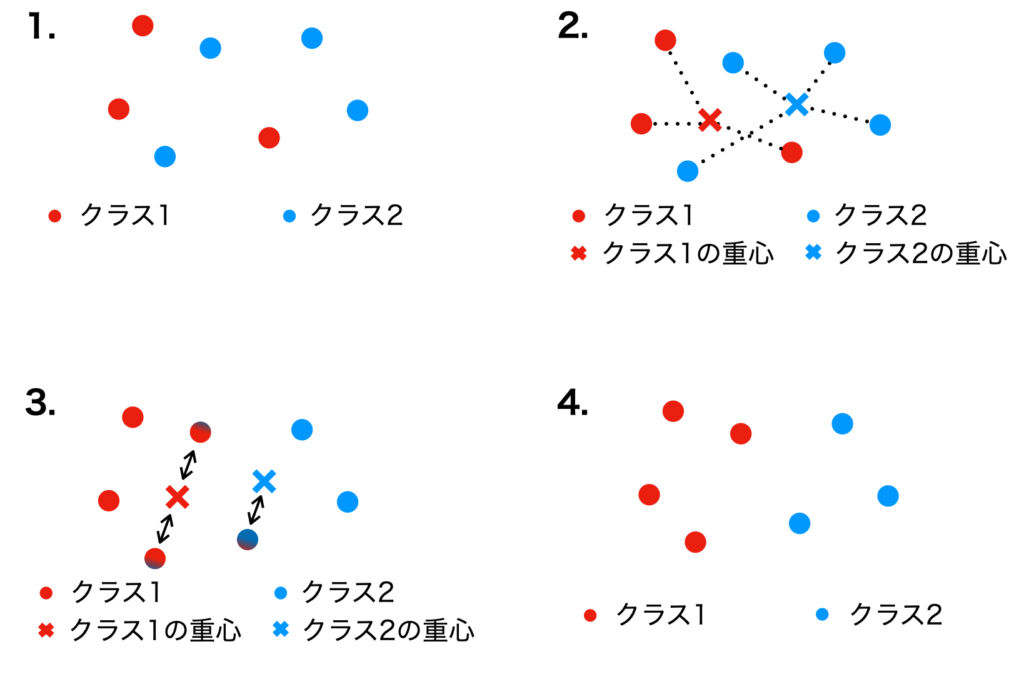
上記アルゴリズムの流れのイメージ図が下の図です。
k-means法の実装
実際にk-means法をpythonを用いて実装してます。注意として、2次元空間上の点に限って議論を進めます。
用いるライブラリは以下の2つです
import numpy as np
from collections import Counter
import copy
np.random.seed(32)実装コードは以下の通りです。
#データ間の距離(ユークリッド距離)を計算する関数.
def distance(p1, p2):
return np.sum((p1-p2)**2)
#k-means法の実装コード
def My_kmeans(k, X):
#------------------
#k: 分類するクラス数
#X: データ点のnp.array
#-------------------
#1. データ点をランダムにk個のクラスに割り振る
init_labels = np.random.randint(0,k, len(X), )
#2. 重心の初期値を計算
tmp_centroids = np.zeros([k,2])
for i in range(k):
tmp_centroids[i] = X[init_labels==i].mean(axis=0) #各クラスの重心を計算
#最大何回計算を繰り返すか
max_iter = 100
#イテレーション毎に変更したデータ点のラベルを管理する
cluster = copy.deepcopy(init_labels)
#重心の変化がなくなるまで、もしくは最大イテレーション回数まで繰り返す
for iter in range(max_iter):
centroids = copy.deepcopy(tmp_centroids)
#3. 各データ点と重心の距離を計算し、データ点を一番近い重心のクラスに割り当てる
for x_index, x in enumerate(X):
dists = np.array([distance(x , centroids[i]) for i in range(k)] )#各重心とデータ点pとの距離を比較
min_dist_index = np.argmin(dists)
cluster[x_index] = min_dist_index
#cluster内のクラス数がk未満になった場合、すなわち空のクラスが存在する場合には
#重心が計算できなくなる場合がある.
#そのため、点が最も多いクラスから1点を取り出し、空のクラスに割り当てる
if len(np.unique(cluster)) < k:
#どのクラスが存在していないかチェック
for i in range(k):
if not i in np.unique(cluster):
#個数が最も多いクラスから一点取り出す
max_cnt = max(Counter(cluster))
indexes = np.where(cluster==max_cnt)[0]
rand = np.random.choice(indexes, 1)
cluster[rand] = i
#4. 新しい重心を計算
for i in range(k):
centroids[i] = X[cluster==i].mean(axis=0)
#重心のリストが変化しなかったら、計算終了
if np.allclose(centroids, tmp_centroids):
break
#重心の座標を更新
tmp_centroids = centroids
return cluster, tmp_centroids
プログラムのテスト
上記プログラムの動作を確認します。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeansテストに用いるデータは以下のコードで作成しました。
X, _ = make_blobs(400, 2,centers=3) #2次元空間に、3つのクラスの400個のデータ点を生成
plt.scatter(X[:,0], X[:,1]) #表示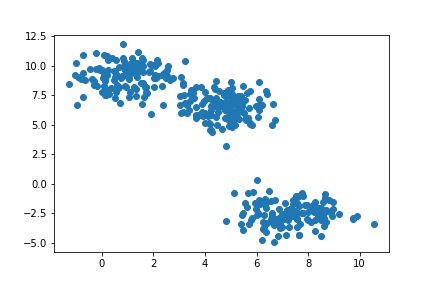
このデータに対して、自作のk-menas法を適用します。
k = 3 #3つのクラスタに分類するように指示
cluster, centroids = My_kmeans(3, X)
for i in np.unique(cluster):
points = X[cluster==i]
plt.scatter(points[:,0], points[:,1], label=f'{i}')
plt.legend()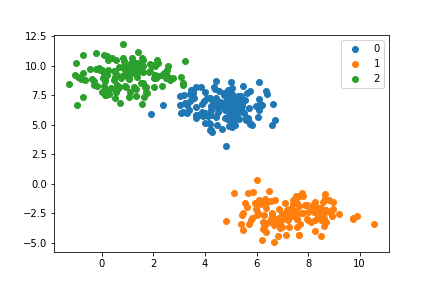
3つのクラスに分類できました。
sklearn.KMeansの実行
比較のため、sklearnのk-means法も実行してみます。
pred = KMeans(n_clusters=3).fit_predict(X)
for cls in np.unique(pred):
ps = X[pred==cls]
plt.scatter(ps[:,0],ps[:,1], label=f"{cls}")
plt.legend()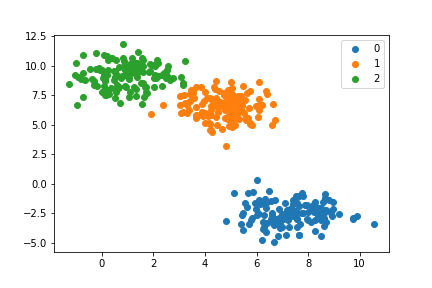
クラスの番号と色の対応が微妙に異なりますが、おおよそ同じ結果を得ることができました。
分類するクラス数を増やした場合
今までは$k=3$でしたが、同じデータに対して $k=10$ に増やして比較してみます。
cluster, centroids = My_kmeans(10, X)
pred = KMeans(n_clusters=10).fit_predict(X)
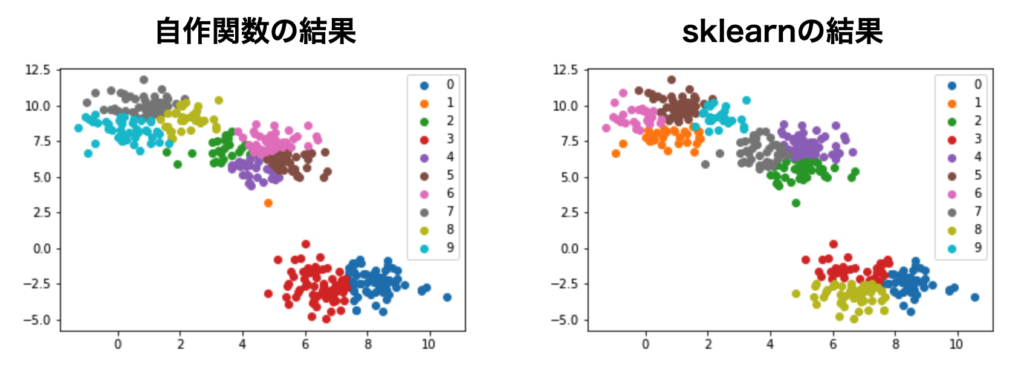
左の図が自作関数の結果で、右がsklearnの結果です。10個のクラスに分類できたのは確認できますが、分類の仕方が微妙に異なっています。
元々クラス数が3個になるよう生成したデータ点を無理矢理10個に分割しているため、初期値のクラス割り振りの違いが影響しているのかもしれませんが、詳細な原因はわかりません。
少なくとも、指定のクラス数に分類できたということは確認できました。
まとめ
k-means法のアルゴリズムのイメージと実装について取り組みました。このアルゴリズムを一言で言えば、データ間の距離の近さを基準に $k$ 個のクラスタ(クラス、まとまり)に分類する手法です。

この書籍も参考にしました。

コメント