[k近傍法] 分類・回帰の仕組みとpythonでの実装

k近傍法(k-nearest neighbor, kNN)は分類・回帰のいずれにも適用できるアルゴリズムです。

このアルゴリズムの原理を一言でいうと、『k個の近隣の点を使って多数決をとる』です。

分類について
回帰について
kNN法を実装してみる
実装コードの確認
まとめ・参考

分類について

例として、以下の絵を使って考えてみます。この絵には赤と青の2クラスのデータが存在しています。これらのすでにクラスが判明しているデータを学習データと呼びます。

黒点が入力データで、今からどのクラスに属するのか考えるデータです。

$k=3$ の場合、点線内の点が黒点(入力データ)に最も近い3つの点となります。この３点のクラスは、

赤2個に対し、青1個となっています。よって、入力データは赤クラスに分類されることになります。

対して、$k=7$ の場合は、赤3個に対して青4個となります。よって、黒点(入力データ)は青クラスに分類されます。

このように、選ぶkの値によって入力データの分類が変わるということに注意する必要があります。

回帰について

回帰の場合も原理は分類の場合と同様です。

入力値に最も近い点の値をとってきて推定値を決定します。

以下の絵は $k=3$ の場合を表しています。入力値に最も近い３点をとってきて、3点の $y$ の値の平均を予測値として採用します。

上の図では、$x$ 軸が説明変数で、$y$ 軸が目的変数を表しています。

入力データ(今わかっている値)が説明変数で、そのデータから得られる予測したい値が目的変数ということができます。

kNN法を実装してみる

kNNの分類アルゴリズムを自分で作成してみます。簡単のため、クラス数は3として進めていきます。

実装の流れは以下の2ステップです。

入力データと学習データの距離を計算
入力データに最も近いk個のデータ点を取得
多数決を採る

#kNNの実装コード
def kNN(input, k):
  #input: 入力データ (1点のみ),
  #k: 何個のデータを用いて多数決をとるか

  #1. 入力データと学習データの距離を計算
  dist = np.sum((X - input)**2, axis=1) #各点との距離を計算
  dist_label = np.c_[dist, Y] #[距離, ラベル]の形状に変形する
  
  #2. 距離が小さい順に並び替え、上位k番目までを採用
  sort_dist_label = dist_label[np.argsort(dist_label[:, 0])]
  k_neibors = sort_dist_label[:k]

  #3. 多数決をとる
  cls_num = [0,0,0] #それぞれクラス0,1,2の個数
  for _, neibor_label in k_neibors:
    
    cls_num[int(neibor_label)] += 1
  
  ans = np.argmax(cls_num) #クラスの個数が多いものを選択
  print(f"入力データのクラスは {ans} です")
  return

実装コードの確認

# 利用したモジュール
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier

上記のコードがきちんと判定をしてくれるか確認します。

まずは学習データを作成します。作成にはsklearn.make_blobs()を利用します。１行でテストデータを作成できるので、とても便利な関数です。

#データ点の作成
X, Y = make_blobs(100, n_features=2, centers=3, center_box=(-5,5), random_state=1)

#作成したデータの可視化
for c in np.unique(Y):
  plt.scatter(X[Y==c,0], X[Y==c,1], label=c)
plt.legend()
plt.title('test data')

$k=3$の場合について、入力データ$(-4, -3)$を代入するとクラスは2と判定されました。

print( kNN(np.array([-4,-3]), 3) )
# 入力データのクラスは 2 です

$k=5$の場合、今度はクラス1と判定されました。

print(kNN(np.array([-4,-3]), 5))
# 入力データのクラスは 1 です

入力データ$(-4, -3)$をプロットすると、確かにクラス1と2の近くに存在していることが確認できます。

for c in np.unique(Y):
  plt.scatter(X[Y==c,0], X[Y==c,1], label=c)
plt.scatter([-4],[-3], label='input')
plt.legend()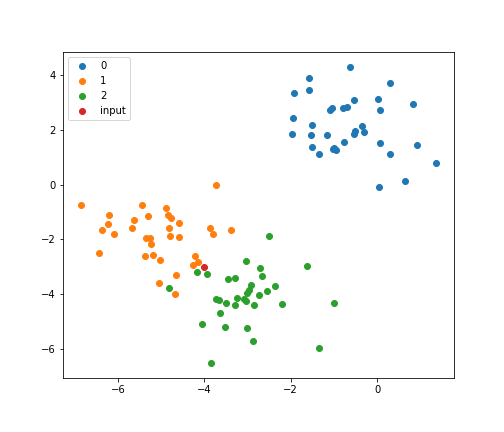

## k=3の場合
neigh3 = KNeighborsClassifier(n_neighbors=3)
neigh3.fit(X,Y)
print(neigh3.predict([[-4,-3]]))
#[2] 

neigh5 = KNeighborsClassifier(n_neighbors=5)
neigh5.fit(X,Y)
print(neigh5.predict([[-4,-3]]))
#[1]

比較のため、sklearn の関数も使って答えを見てみます。

sklearnでも自作コードと同じく、$k=3$の場合はクラス2が、$k=5$の場合はクラス1が出力されました。