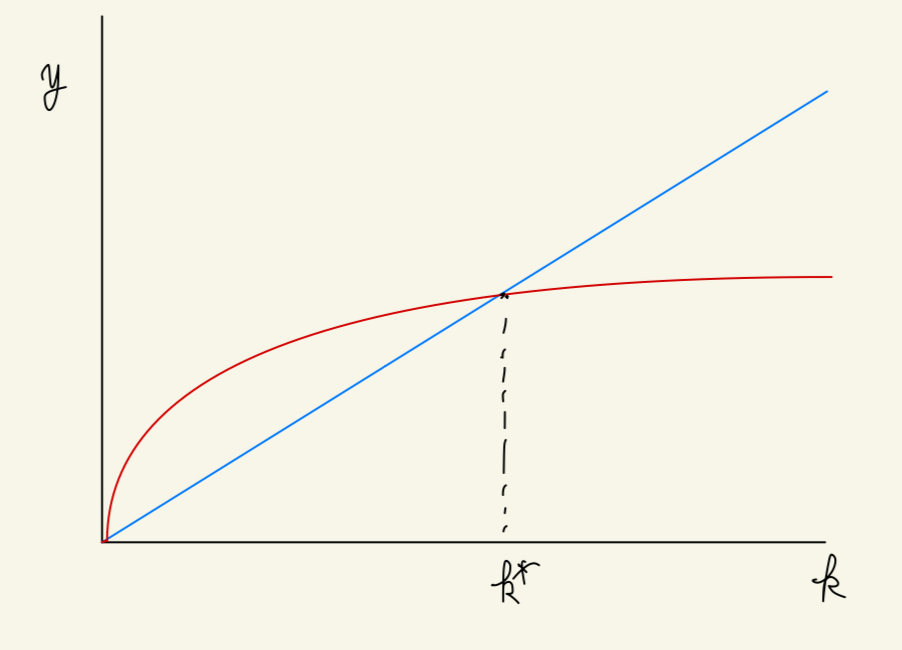
経済学の本を読んでいて成長経済理論の「ソロー=スワンモデル」について学んだのでメモ
結論
・一人当たりのGDPはある均衡点で定常化する(技術革新を一定にした場合)。そのため、先進国ほど技術革新の必要性が増すという結論を導くことができる。
・一人当たりGDP=一人当たりの平均給与は人口が少ない方が多くなる。そのため、中国の一人っ子政策は、一人当たりの平均給与を高める効果につながると理論的に解釈することができる。
基礎方程式の導出
マクロの生産関数を以下の式で定義します。
$Y=A F(K, L)$
$YをGDP、 Fが生産関数、K が資本、Lが労働力$となる。
ここで両辺を 労働力 $L$ で割ることで、変数の個数を1つにします。
$ y = a f(k)$
$y=Y/L, k=K/L$ となり、それぞれ一人当たりのGDP, 資本という意味に解釈できる。
以下、生産性$a$は定数と仮定して論を進める。
ここで $k$ の変化量に着目すると、
$\frac{\Delta k}{k} = \frac{1}{K} \Delta(KL)$
この式をまとめると、
$\frac{\Delta k}{k} = \frac{\Delta K}{K} – \frac{\Delta L}{L} $
つまり、一人当たりの資本量を増やすには、
- 資本量を増やす
- 労働量を減らす(=人口を減らす)
という式であると解釈ができる。
ここで、右辺第二項目から、人口が減ることで一人当たりのGDP(=給与)が増えると解釈でき、一人っ子政策の理論的な支えになっていると解釈できる。
さらに分解してみる
$\Delta K$ の部分をさらに分解してみます。
まず、 $ K \propto sf(k) $ と変形できます。($s$ は貯蓄率を意味します)
こうなる理由としては、
「貯蓄は投資(=I)になり、その投資は資本(=K)となる」
という考え方に即して変形されます。すなわち、
$K = I = sY$
さらに、資本 $K$ は時間と共に価値を減らす(=減耗)も含める必要があります。その分を$\delta K$とすることで、
$K= sY – \delta K$
と書くことができます。
以上から、$K=kL$であるため、
$\frac{\Delta K}{K} = (sY – \delta K)/K = \frac{s}{k}\frac{Y}{L} -\delta $
ただし、$\delta = \frac{\delta K}{K}$ としています。
一人当たりの資本量 に戻ると、$y=Y/L, n = \frac{\Delta L}{L}$より、
$\Delta k = sy – (\delta k + n)k $
基礎方程式をグラフで見る
上記手続きで得られた右辺の式をプロットしてみます。
$\Delta k = sy – k(\delta k + n) = sf(k) – (\delta + n)k $
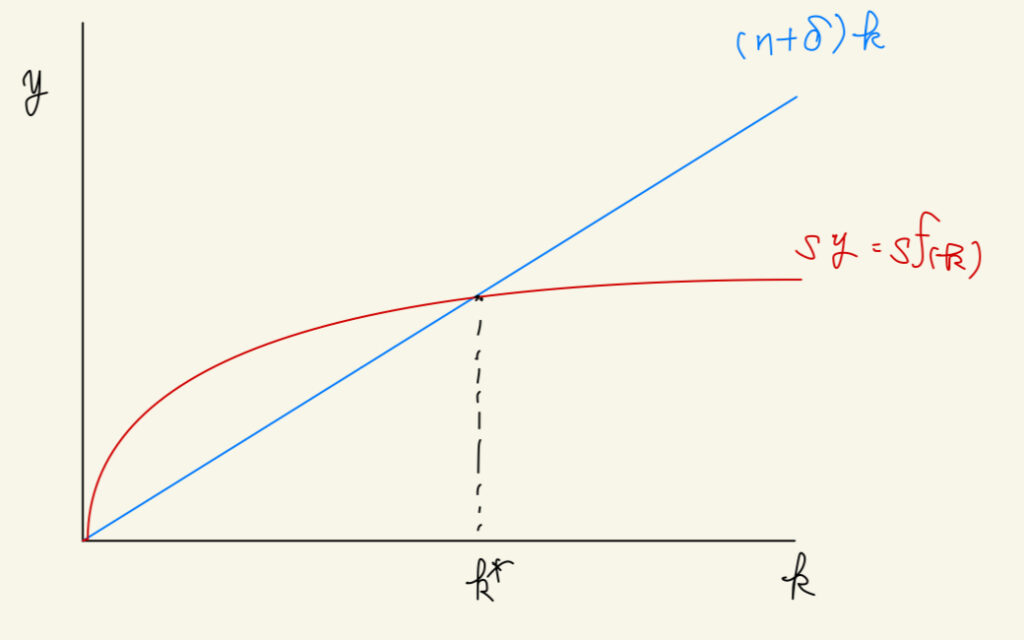
一人当たりの総資本 $k$ が交点 $k^*$ よりも左側にある場合、資本を増やす力>資本を減らす力となあります。そのため、貯蓄が投資に回ることで一人当たりの資本が増え、それによって一人当たりのGDPが増えていくといえます。
また、交点 $k^*$ よりも右側にある場合、一人当たりのGDPを減らす方が優勢となるため、交点 $k^*$へ戻ってしまうと解釈できます。
以上より、このモデルに従うと、経済成長ある一定値で止まってしまうと解釈できます。
この状況は、最初の仮定である $a=一定$ により発生しており、この値が技術革新で生産性を上げることで更なる経済成長へ繋げることができると導くことができる。
感想
現在日本が先進国の中でも低成長で、その主原因の一つにIT化の遅れがある、DX化を推進していく必要があるとの言説を目にすることがあります。この主張の理論的基盤として、このソロースワンモデルの結論があると思いました。
日頃ニュースで取り上げられている言説の根拠、理論基盤に触れることができた気がしてとても印象的な理論でした。
何か参考になれば幸いです。