本記事の内容は主に以下の3点
- pythonによるダイクストラ法の実装コードの提示(コピペで使えるコード)
- 簡単なグラフを用いたアルゴリズムの流れの可視化
- 経路復元の方法
コード
ヒープを用いたダイクストラ法が以下となります。
import heapq
inf = float('INF')
def dijkstra(s, G):
"""
s:スタート地点
G: 隣接グラフ [ [(v0,d0),...,(vj, dj)],..., [(v2,d2)]]
"""
n = len(G) #頂点数
dist = [inf]*n #スタート地点からの距離のリスト
dist[s] = 0 #スタート地点
seen = [False]*n #探索済みかどうか管理
hq = [(0,s)] #ヒープの都合上、(距離, 頂点番号)の並び
heapq.heapify(hq) #ヒープ化
while hq:
v = heapq.heappop(hq)[1] #次のノード
seen[v] = True
for to,cost in G[v]:
if seen[to]==False and dist[v]+cost < dist[to]:
dist[to] = dist[v]+cost
heapq.heappush(hq, (dist[to], to))
return distヒープを用いているため、計算量は $O(E \ \mathrm{V})$ となる。
アルゴリズムの流れ
以下のグラフをダイクストラ法で解く流れを可視化します。緑の点が頂点で、0から3までの番号をふっています。また、矢印が有効グラフで、距離(コスト)が付随しています。
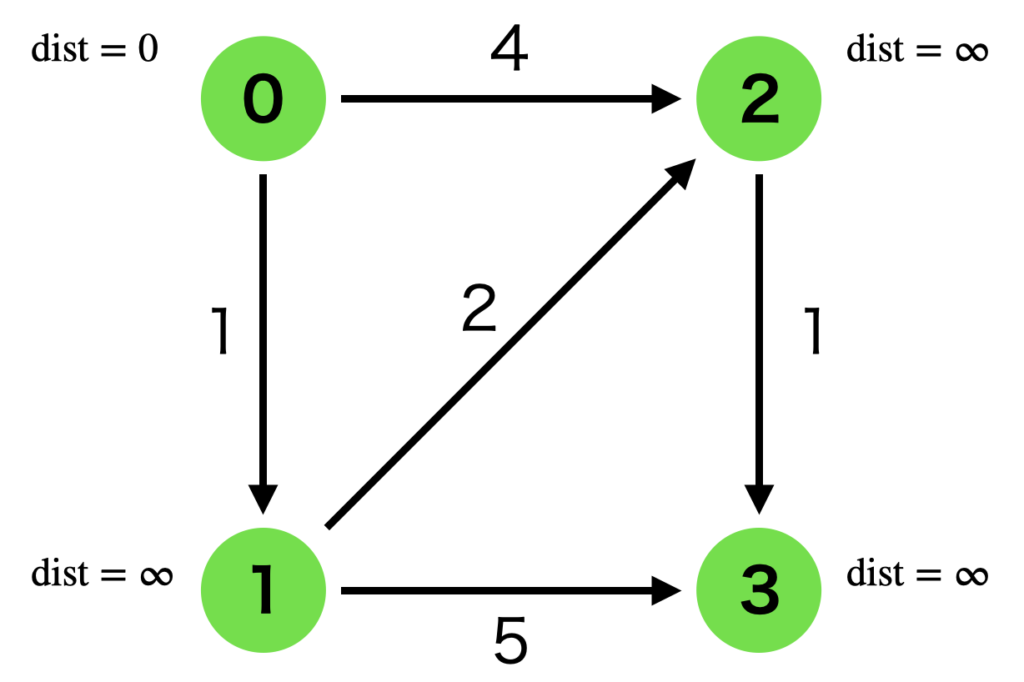
スタート地点を頂点0とし、頂点0の到達距離を dist=0 とします。
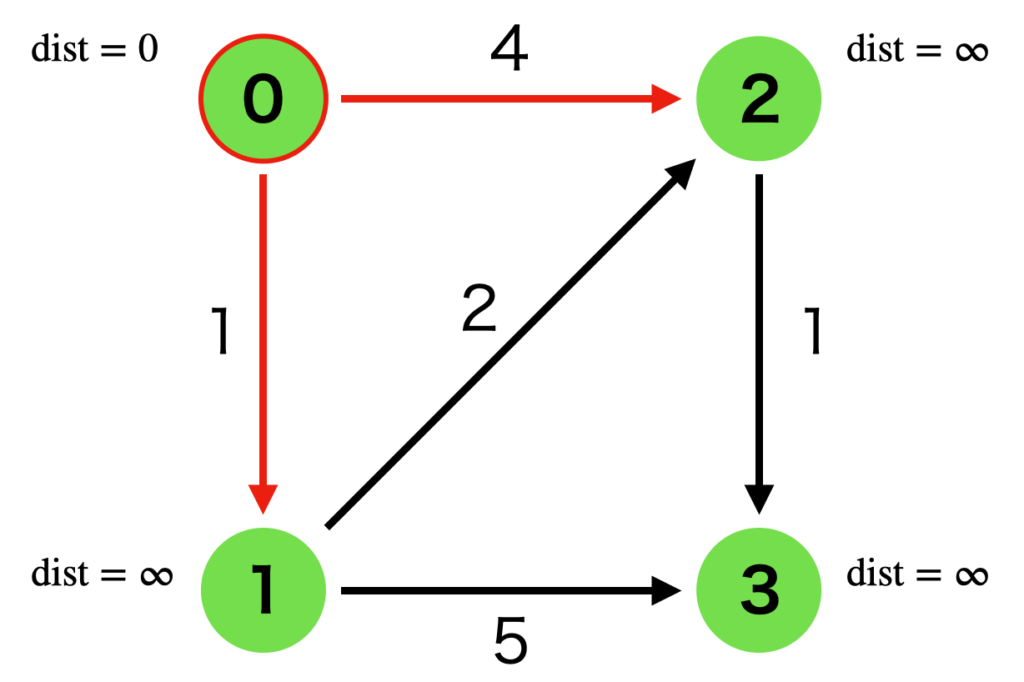
頂点0から進める辺2つあります。
- 頂点2への距離4の辺
(4,2) - 頂点1への距離1の辺
(1,1)
ただし、(距離,頂点番号) で管理しています。
このうち、距離が最小の (1,1) を採用し、頂点1の到達距離を dist=1 に更新します。
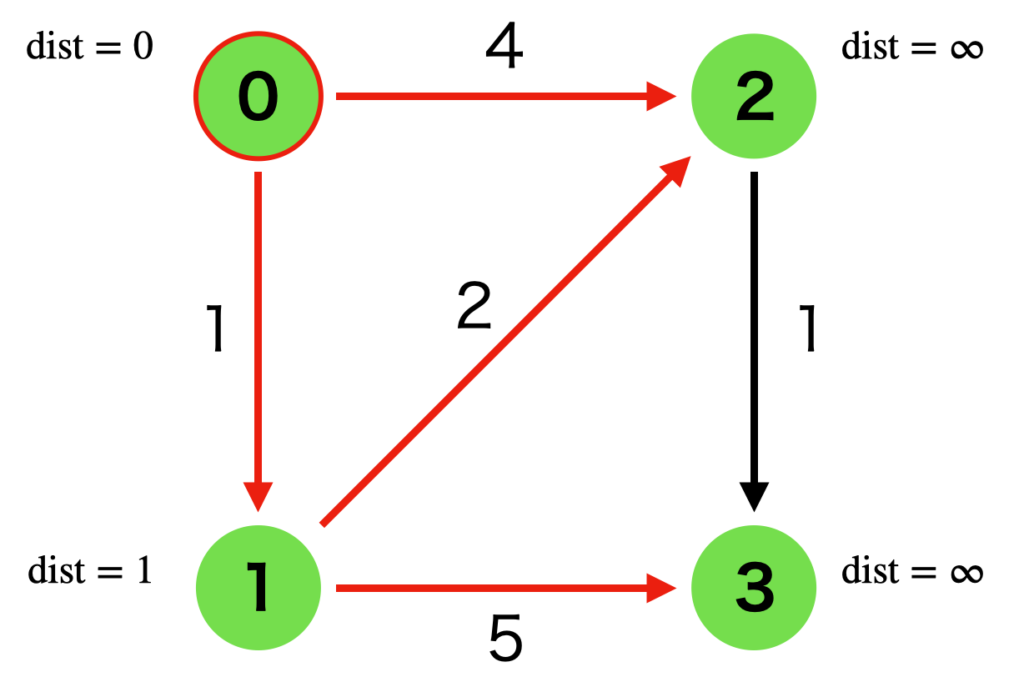
次に、探索済みの頂点0と頂点1からたどれる3つの辺 (4,2), (3,2), (6,3) が経路の候補となります。ただし、今は頂点0からの最短経路を考えているため、(3,2), (6,3) の距離には頂点0->頂点1へのコスト1が加算されています。
これら3つの辺のうち、距離が最小の (3,2) を採用し、頂点0から頂点2へ進みます。
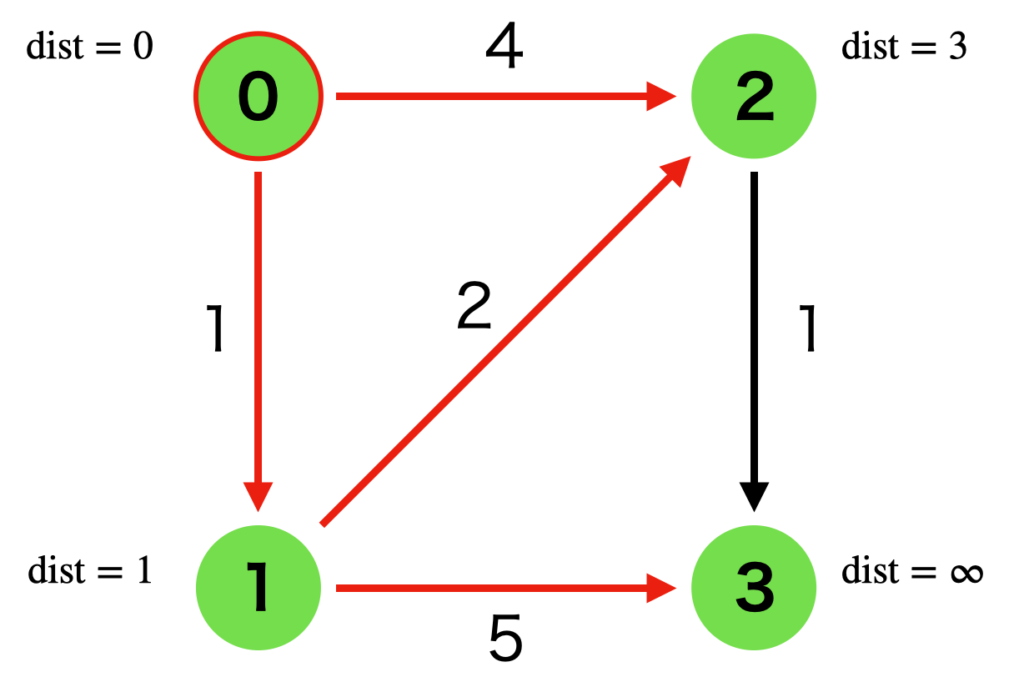
次に、探索済みの頂点0, 1, 2からたどれる辺 (4, 2), (4, 3), (6, 3) が経路の候補となります。
このうち、(4, 2) に関しては、頂点2が探索済みのため無視します。残りの2辺 (4, 3), (6, 3) から距離が最小の (4, 3) を採用します。
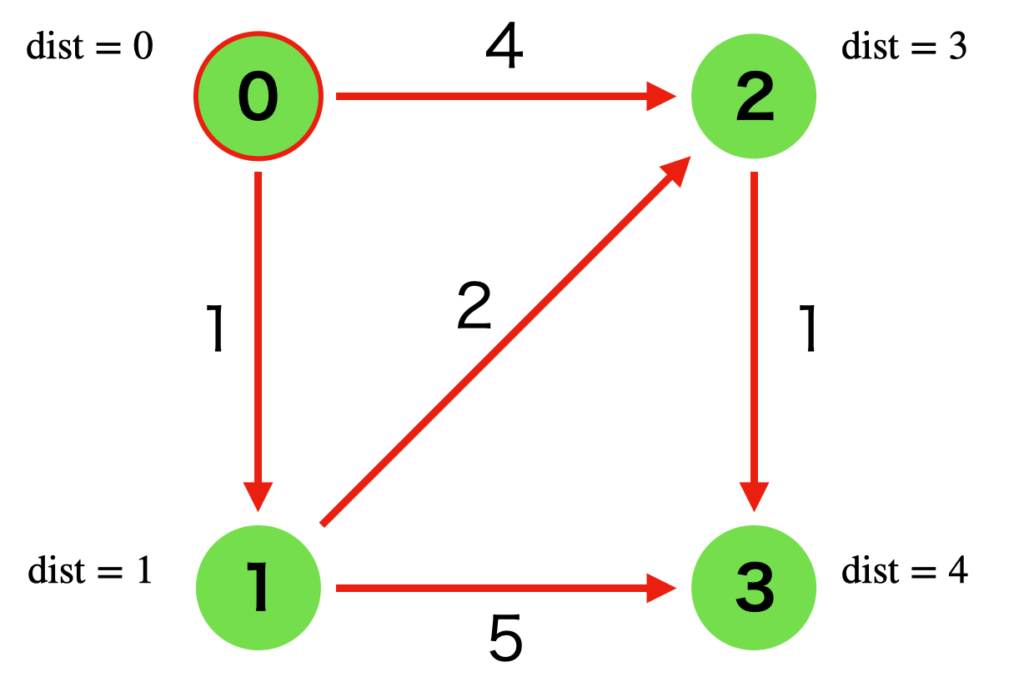
すべての頂点が探索済みとなり、ダイクストラ法が完了しました。
ちなみに、この流れをコードで実装すると、
G = [[(1, 1), (4, 2)], [(2, 2), (5, 3)], [(1, 3)], []]
dists = dijkstra(0, G) #スタート地点 0
for i in range(len(dists)):
print(f"頂点{i} への距離は {dists[i]}")
#頂点0 への距離は 0
#頂点1 への距離は 1
#頂点2 への距離は 3
#頂点3 への距離は 4経路復元の方法
ダイクストラ法のコードに管理するリスト prev を増やすと、ゴール地点までの経路を求めることができるようになります。prev はあるノード v の直前のノード番号 u を管理します。
import heapq
inf = float('INF')
def dijkstra(s, G):
"""
s:スタート地点
G: 隣接グラフ [ [(v0,d0),...,(vj, dj)],..., [(v2,d2)]]
"""
n = len(G) #頂点数
dist = [inf]*n #スタート地点からの距離のリスト
dist[s] = 0 #スタート地点
seen = [False]*n #探索済みかどうか管理
prev = [-1]*n #経路復元用のリスト.直前までいたノード番号を管理
hq = [(0,s)] #ヒープの都合上、(距離, 頂点番号)の並び
heapq.heapify(hq) #ヒープ化
while hq:
v = heapq.heappop(hq)[1] #次のノード
seen[v] = True
for to in G[v]:
#未探索 かつ 行先のコストが小さくなる場合 は更新
if seen[to]==False and dist[v]+1 < dist[to]:
dist[to] = dist[v]+1
prev[to] = v #ノードtoに到達する直前にいたノードがv
heapq.heappush(hq, (dist[to], to))
return dist,prev
#prevから頂点tへの経路を計算する
def get_path(t, prev):
path = []
while t !=-1:
path.append(t)
t = prev[t]
#ゴールからスタート地点へ遡る形のため、
#順番を反転させて返す
return path[::-1]実行例
G = [[(1, 1), (4, 2)], [(2, 2), (5, 3)], [(1, 3)], []]
dist, prev = dijkstra(0, G) #スタート地点 0
path = get_path(3, prev) #dijkstraで得られたprevを用いて3へのノードを計算
print(path)
#[0, 1, 2, 3] #頂点0->頂点1->頂点2->頂点3の順番に到達した。まとめ
ダイクストラ法を用いた最短経路問題についてコードをまとめました。
本記事のコードはコピペするだけで使えるようになっています。また、上記コードは AIZU ONLINE JUDGE GRL_1_A で正解になることを確認しました。
最短経路を求める他のアルゴリズム(ベルマンフォード法、ワーシャルフロイド法)については以下の私の記事でも述べています。ご興味があればぜひ。
参考
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年


コメント