ベルマンフォード法の実装コードに関するメモです。
ポイント
- 負の重みを持つグラフに対して最短経路の計算を実行できる。
- 負の閉路の有無の判定が可能
- 計算量は $O(E V)$です。( $E, V$ はそれぞれ辺の本数と頂点の個数)
- 負の重みがグラフになければ、ダイクストラ法の方が高速
コード
inf = float('INF')
def BellmanFord(G, s):
"""
s:スタート地点
G: 隣接グラフ [ [(v0,d0),...,(vj, dj)],..., [(v2,d2)]]
返り値
dist: 頂点sからの最小コストを管理しているリスト
negative_cycle: True/False (負の閉路を持つか否か)
"""
n = len(G) #頂点数
costs = [inf]*n #頂点sからの到達コストを管理するリスト
negative_cycle = False
#スタート地点
costs[s] = 0
for i in range(n):
update = False #更新の有無
#各頂点
for v in range(n):
#頂点vから出る辺の重みをみる
for to, c in G[v]:
if costs[to] > costs[v] + c:
costs[to] = costs[v]+c
update = True
if update == False:
break
if i==n-1 and update==True:
negative_cycle = True
return costs, negative_cycleアルゴリズムの流れ
以下のグラフを用いてベルマンフォード法の流れを考える。緑丸が頂点を表し、0から3までの番号がふられている。また、各頂点からのびている矢印は有向辺を意味し、その重みが書かれている。
以下、有効辺に関しては 左が始点で右が終点のベクトルとして表記します。例えば、頂点0から頂点1への有向辺は $\vec{01}$ とします。
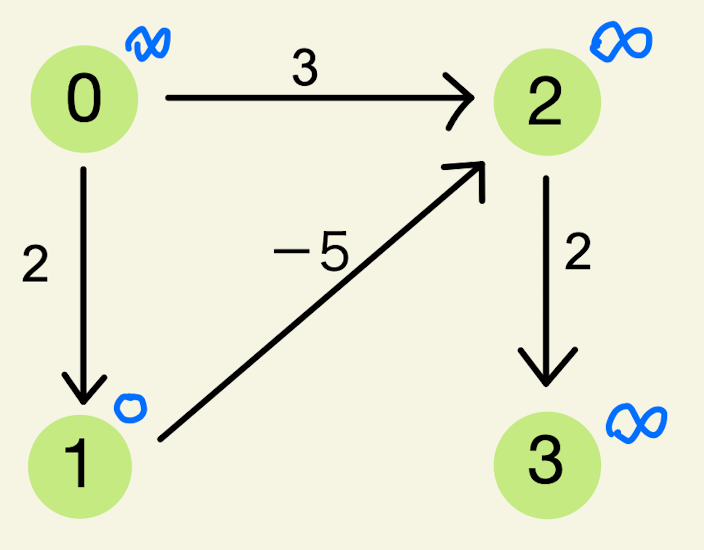
頂点1からスタートして各頂点に行くまでのコストを考えます。
ベルマンフォード法では、4つすべての辺 $\vec{02}, \vec{01}, \vec{12}, \vec{23}$ に関してコストの更新を試みます。
$\vec{02}$ の場合
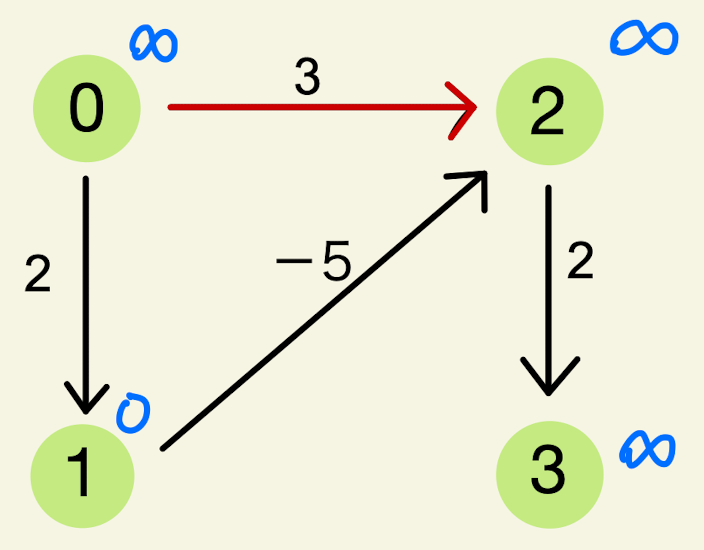
赤い辺に関して考えます。costs[2]=∞, costs[0]+3=∞ で、costs[2]>costs[0]+3 を満たさないため、この辺によるコストの更新は行いません。
$\vec{01}$ の場合
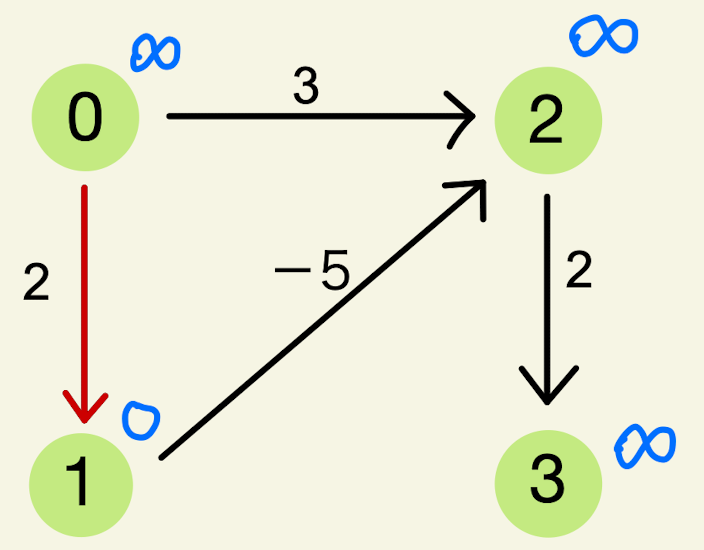
$\vec{02}$ の場合と同様に更新は行われません。
$\vec{12}$ の場合
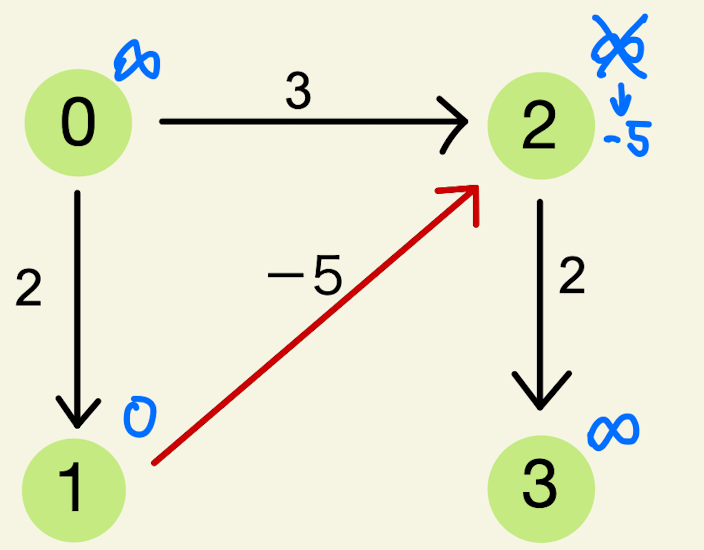
costs[2]=∞, costs[1]+(-5)=-5 で costs[2]>costs[1]+(-5) を満たすため、到達コストの更新が行われます。すなわち、costs[2]=∞ から costs[2] = -5 へ変更されます。
$\vec{23}$ の場合
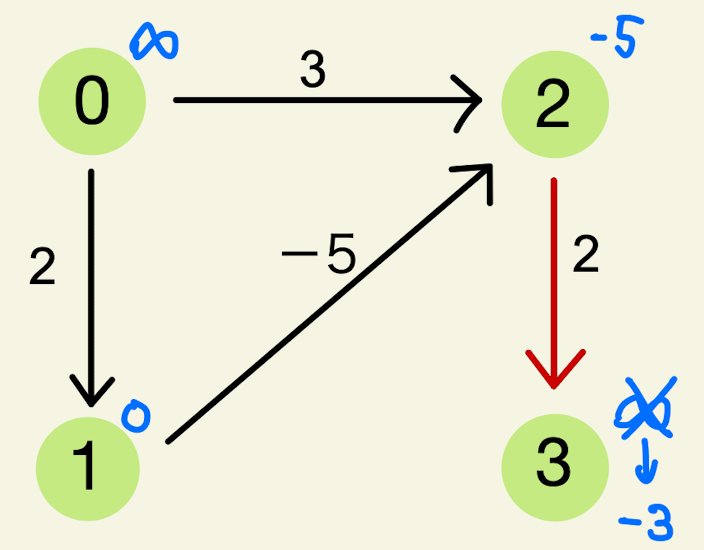
costs[3] > costs[2]+2 を満たすため、コストの更新が行われます。 costs[3]=∞ から costs[3] = -3 へ変更されます。
以上、4つの辺に関してコストを更新していく作業を頂点の個数回(今回は4回)だけ繰り返します。
頂点の個数回繰り返した場合にもコストの更新がされた場合、負の閉路があるとみなされます。
図1のグラフを今回作成した関数で解くと、以下のようになります。
G = [[(1, 2), (2, 3)], [(2, -5)], [(3, 2)], []] #図1の隣接グラフ
costs, flg = BellmanFord(G, 1) #到達コストを管理するリスト と 負の閉路の有無を表すflg
if flg:
print("NEGATIVE CYCLE")
else:
for i in range(V):
print(f"頂点{1}から頂点{i}までのコスト: {costs[i] if costs[i]!=inf else 'INF'} ")
#頂点1から頂点0までのコスト: INF
#頂点1から頂点1までのコスト: 0
#頂点1から頂点2までのコスト: -5
#頂点1から頂点3までのコスト: -3 補足
今回紹介したベルマンフォード法のコードにおいて、19行目の下に以下のコードを付け足すと、多少高速になります。(図1の例でいうと、$\vec{01}, \vec{02}$ の計算をスキップできるため)
for v in range(n):
#以下のコードを追加する
if costs[v] == inf:
continue まとめ
ベルマンフォード法に関するメモをまとめました。
また、今回作成したコードは AIZU ONLINE JUDGE GRL_1_B にて正解になることを確認しています。
最短経路を求める他のアルゴリズム(ワーシャルフロイド法、ダイクストラ法)については以下の私の記事でも述べています。ご興味があればぜひ。
参考
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年

コメント