本記事のキーワード
- 最適消費
- 無差別曲線
- 2財モデル
- 限界代替率(Marginal Rate of Substitude)
2財モデルとは
消費者の行動を考える上で大事な考え方として,「消費者は自身の満足感を最大化する」ように行動・消費するという仮定を置きます.
この満足感のことを「効用(utility)」と呼びます.
この効用(満足感)を考える上で,現実世界には非常に多様な種類の商品が存在しており,その組み合わせはほぼ無限にあり手に負えません.そこで思い切った簡単化として「2財モデル」が存在します.
2財モデルでは世の中にたった2種類の財(商品)しかないと仮定し,その中での消費の組み合わせ・消費行動を考察します.
2財モデルと効用関数
世の中には2種類しか商品が存在しないと仮定すると,消費者はその2種類しか購入する選択肢がないことを意味します.そのため,消費者の満足度(=効用)は2財の組み合わせで決まることになります.
数学的に言い換えれば,消費者の満足度はx,yの関数として描かれます.
u = f(x,y) # u=utility(効用), x,y: x財・y財の数量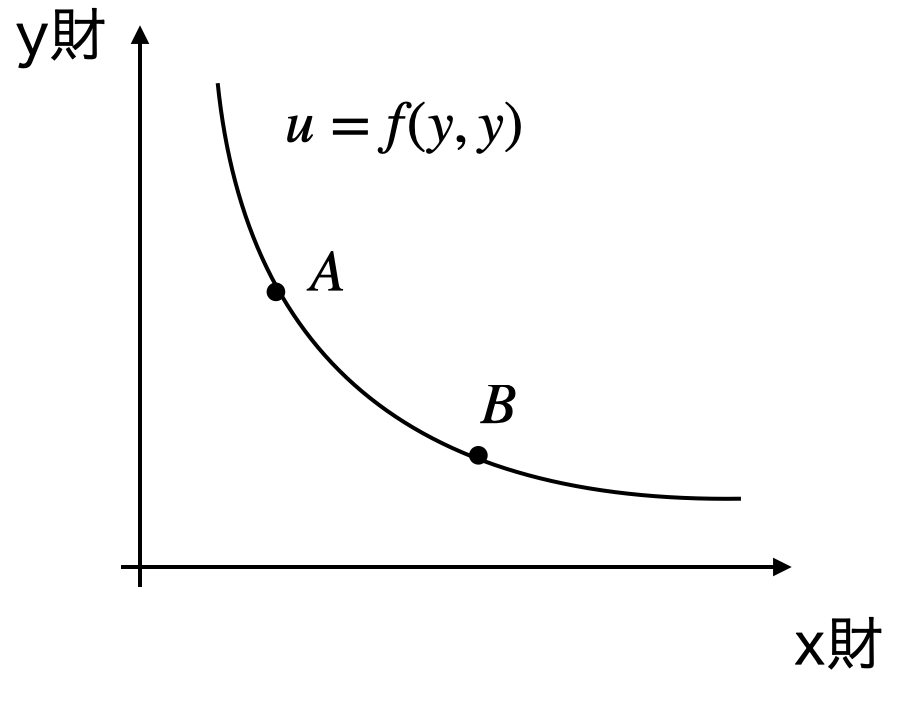
この効用関数にはいくつかの性質があります.
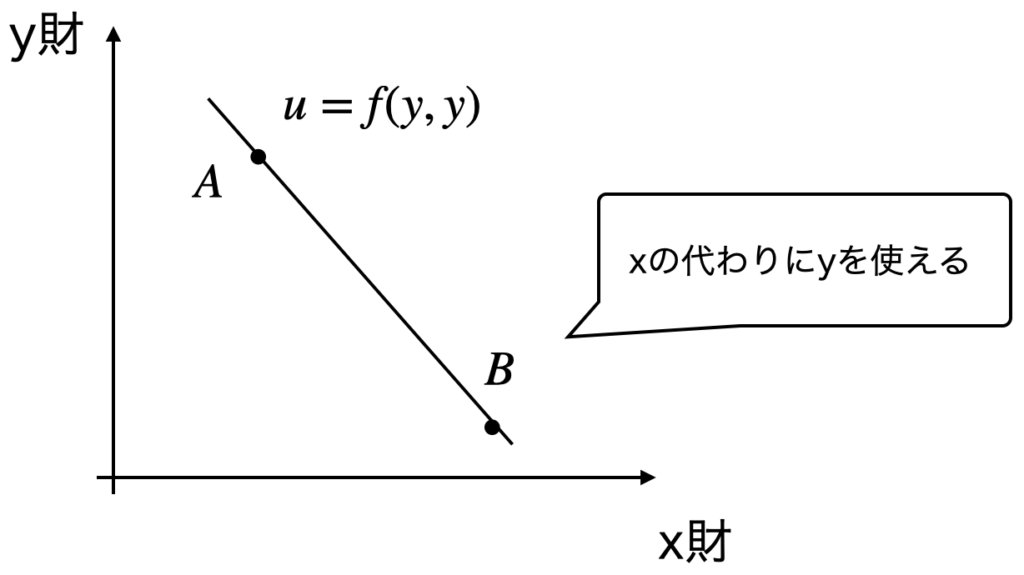
- 同じ曲線上であれば,どの点も効用は等しい(点Aと点Bは同じ効用)
- 一般的に曲線は右下がり
- 原点に対して凸
- 原点から遠いほど効用の値は大きくなる
右下がりな理由:右上がりの場合,xを増やすとyも増えることを意味します.x=ビール,y=ワインとすると,ビールを1杯増やすとワインが1杯増えることになり,これが同じ効用になることは直感と反しています.「片方を増やしたらもう片方は減る」を表現するため,右下がりになります.
限界代替率(Marginal Rate of Substitute, MRS)
簡単に言えば「2財曲線の傾き」に過ぎません
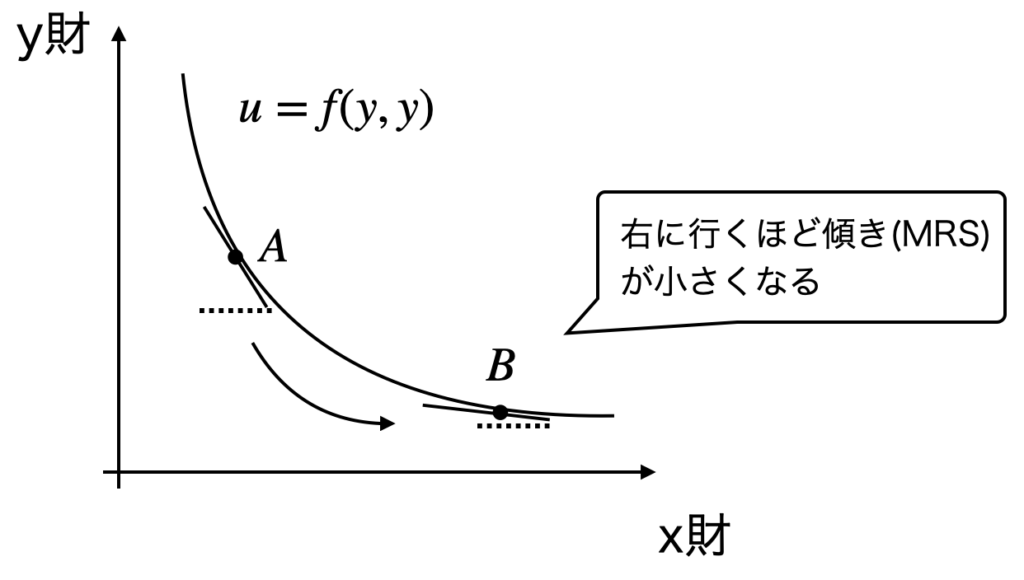
MRS = du/dx MRSの解釈は,「xを1単位だけ増加(or減少)させた際,効用(満足感)を一定に保つためにy財をどの程度減少(or増加)させないといけないか」となります.
効用曲線は一般的に右下がりの性質を持つため,xが極端に大きくなると傾きの絶対値も小さくなっていきます.この性質のことを限界代替率逓減の法則といいます.
無差別曲線の極端な例
完全補完財
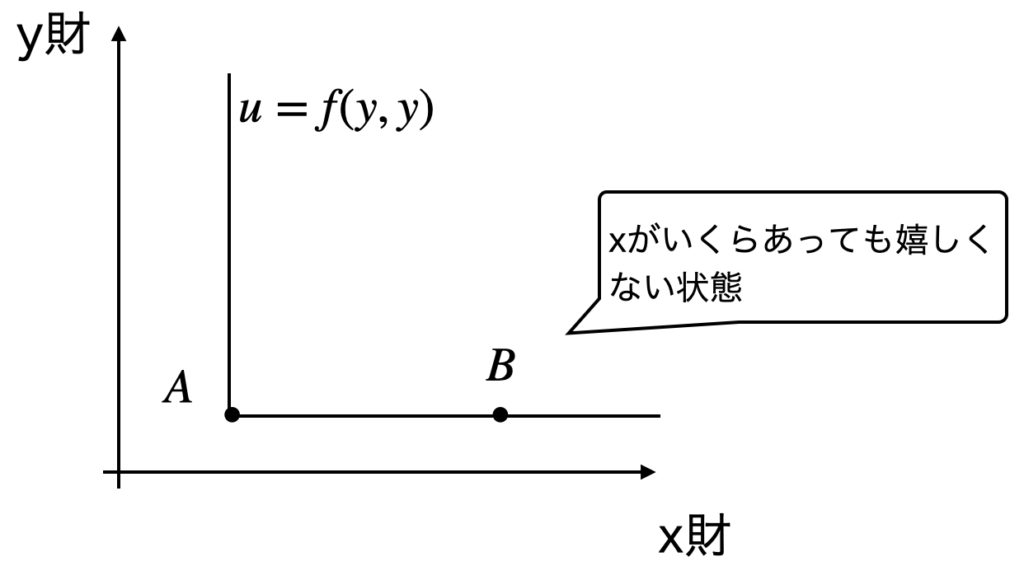
2つで1セットとして使われる財のこと.例えば靴で,左が1つで右が10個あっても全く嬉しくありません.
この財の場合は直角のグラフになります.(右の靴が増えても効用は全く増えない)
完全代替財
2つの財が全く同じ性質を備えている財のこと.例えば角砂糖とスティックシュガーが挙げられ,限界代替率の値はどこも一定,すなわち直線になります.