本記事では、二分探索の応用問題である『値の最大化問題』ついて解法をまとめます。
問題の考え方: コピペ用コード
問題に慣れるまでは、以下の二点に集中すると考えやすいと思います。
- 3行目の条件判定の関数
- 13-16行目の範囲の絞り込み
#1. 条件を満たすか判定する関数
def condition(*arg):
#問題文にあう条件を判定
#2. 二分探索パート
left, right = 0, MAX #下限値、上限値
#解の範囲が十分小さくなるまで繰り返す
for i in range(100):
mid = (right+left)/2 #中間値
if condition(*arg):
left = mid #もしくは、right = mid
else:
right = mid #もしくは、left = midこの二箇所をどうするか考える方針で話を進めていきます。
また、pythonの標準ライブラリに bisect がありますが、本記事では扱いません。
bisect の具体的な使い方に関しては、以下の記事などをご参照ください。
値の最大化問題 1
以下の問題を二分探索で解いてみます。
アルル は $N$本のひもを持っています。
ひもには 0 から $N-1$ までの番号がついており、ひも $i$の長さは $L_i$です。アルルは、これらのひもを切って同じ長さのひもを $K$ 本用意しようと考えています。
アルルが用意できるひもの長さの最大値を求めてください。
ただし、ひも同士を連結させることはできません。答えを出力してください。絶対誤差 (想定解と出力の差の絶対値) は $10^{-6}$ まで許されます。
アルゴ式 Q2-8.ひもを切る
問題の趣旨について
用意できるひもの長さの最大値 $X’$ と仮定します。その時、$X’$以上では本数が $K$ 本未満になり、$X’$ 以下では $K$本以上になることが言えます。
図にすると以下のように書けます。
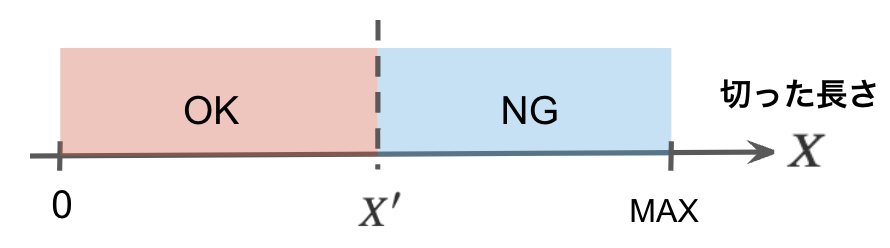
ある値$X’$が存在し、この値を境界に条件を満たす/満たさないが変わります。この$X’$を見つけることがこの問題の課題です。
この$X’$を見つけることが問題の要求です。言い換えると、『条件を満たす最大値』の探索と解釈できます。
判定関数について
切り取ったひもの長さを $X$ と仮定します。ひも $l_i$ からは $\lfloor l_i/X \rfloor$ 本切り取ることができます。
そのため、問題文の要求は以下のように定式化できます。
$$\sum_{i=0}^{N-1} \lfloor l_i/X \rfloor >=K \tag{eq. 1}$$
この式を満たすかどうかの判定関数をコーディングできればokです。
補足ですが、$\lfloor x \rfloor$は小数部分の切り捨てを意味します。例えば、$\lfloor 3.14 \rfloor = 3$ です。
範囲の絞り込みについて
$$\sum_{i=0}^{N-1} \lfloor l_i/X \rfloor >=K $$
この数式を満たす場合を考えます。その場合、$X$はさらに大きい値も取り得るため、大きい方の範囲に絞り込むことが可能です。すなわち、 left = mid と絞り込めます。
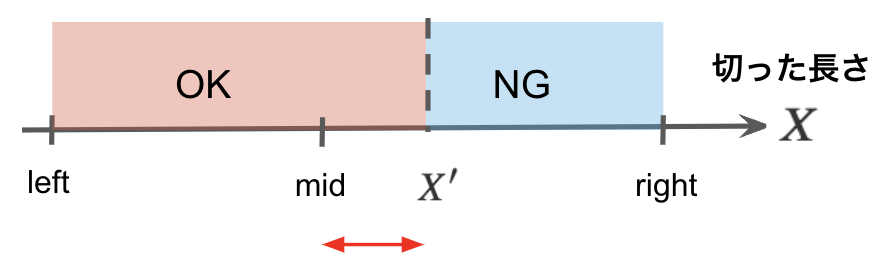
逆に、この式を満たさない場合、$X$ が大きすぎることを意味します。そのため、 right=mid と絞り込み、小さい範囲で値を探索します。

Pythonの解答コード
N,K = map(int, input().split())
L = list(map(int, input().split()))
#1. 条件を満たすか判定する関数
def Condition(X,K):
ans = 0
for li in L:
ans += int(li/X)
#条件:K以上か否か
if ans >= K:
return True
else:
return False
#2. 二分探索パート
left, right = 0, 10**5+1
#解の範囲が十分小さくなるまで繰り返す
while right - left > 1e-8:
mid = (left + right)/2
if Condition(mid, K):
#Xをより長くできる可能性があるため、下限値を上げる
left = mid
else:
#Xが長すぎるため、上限値を小さくして探索範囲を狭める
right = mid
print(left)上記のコードで アルゴ式 Q2-8.ひもを切る をACすることができました。
値の最大化問題 2
AtCoder Beginner Contest 146 C の問題です。
高橋くんは整数を 1 つ買いに整数屋さんに行きました。
整数屋さんには 1 以上 $10^9$ 以下の整数が売られていて、整数 $N$ を買うためには $A\times N + B\times d(N)$ が必要です。ここで、$d(N)$ は $N$ の十進表記での桁数です。
高橋くんの所持金が $X$ 円のとき、高橋くんの買うことのできる最も大きい整数を求めてください。ただし、買うことのできる整数が 1 つもない場合は 0 を出力してください。
AtCoder Beginner Contest 146 C- Buy an Integer
購入できる整数の最大値を探索する問題です。
判定関数について
整数$N$の金額と所持金$X$について、
$$ A\times N + B\times d(N) <= X$$
この式を満たすかどうかの判定関数をコーディングできればokです。
Pythonの解答コード
A,B,X = map(int, input().split())
def condition(a,b,n):
digits = len(str(n))
return a*n +b*digits <= X
left, right = 0, 10**(9)+1
for i in range(100): #while right - left > 1: としてもok
mid = int( (right + left)/2 )
if condition(A, B, mid):
#midよりたくさん買える可能性がある
left = mid
else:
#midが高すぎるため低くする
right = mid
print(left)ちなみに、答えの最大値が$10^9$ のため、最悪でも$\mathrm{log_2}(10^9) \sim 30$ 回の繰り返しで答えに辿り着きます。したがって、for文 の100回ループは十分と言えます。
上記のコードで AtCoder Beginner Contest 146 C- Buy an Integer でACできたことを確認済みです。
まとめと参考
二分探索の応用問題の考え方と実装コード例についてまとめました。
慣れるまでは、コピペ用コードの1.判定関数 と 2.範囲の絞り込み を集中的に考えると理解しやすいと思います。
他にも問題があると思うので、適宜追加していきたいと思います。





