多角形が凸か否かの判定アルゴリズムについて解説します。
凸多角形とは
凸多角形を一言で言えば、図形内部にどんな線分を置いても外部にはみ出さない図形です。
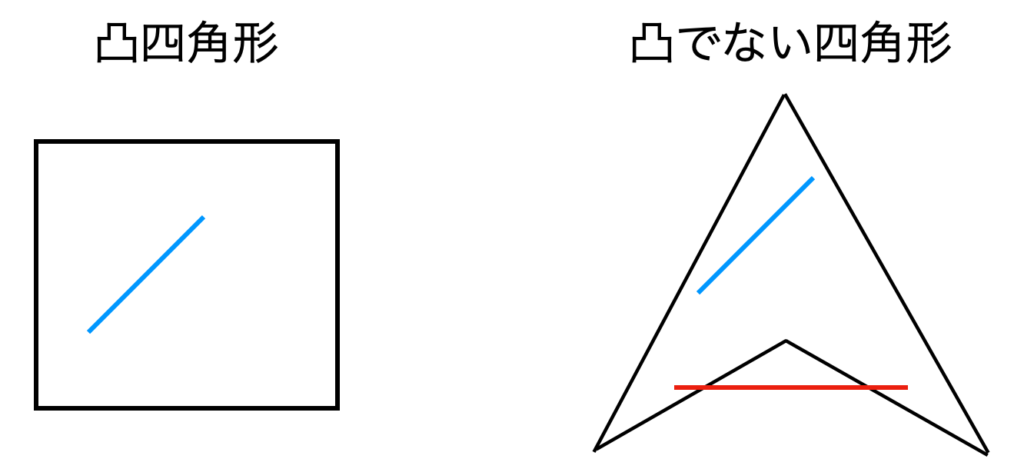
この左の図形か、もしくは右の図形かを判定するのが今回のアルゴリズムとなります。
アルゴリズムの内容
注目する凸多角形の性質
凸多角形の性質の一つに、以下のものが挙げられます。
反時計回り(もしくは時計回り)だけで図形を一周できる
凸四角形と凸でない四角形で比較してみるとよりわかりやすいと思います。
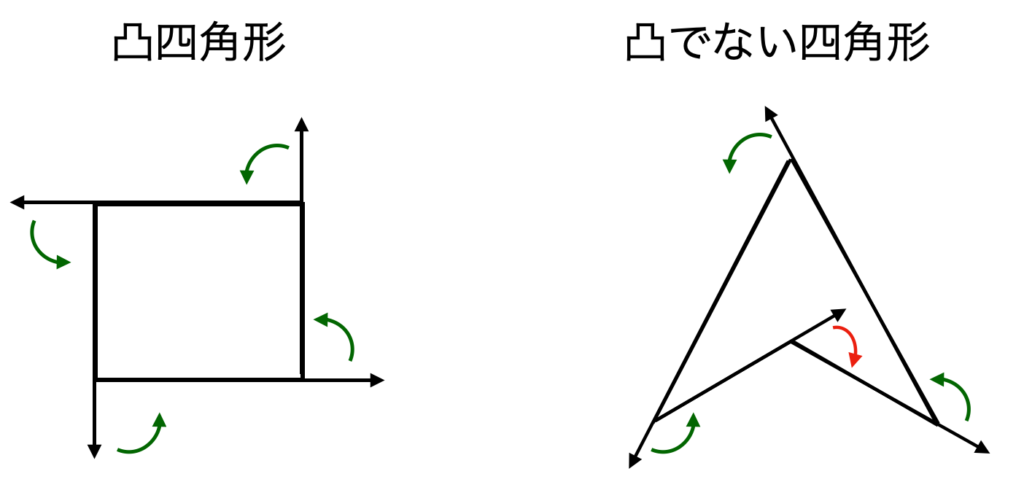
この性質を言い換えると、反時計回りに一周するとき、次に進む辺が進行方向の左手側に現れます。逆に、凸でない図形の場合は進行方向の右手側に進む辺が現れる部分が存在します。
左手側・右手側の回転を数学的に計算する方法として、外積 を利用することができます。
def cross(x1,y1,x2,y2):
return x1*y2 - x2*y1
#もし正の値であれば、左回転
#負の値であれば、右回転pythonでの実装コード
def cross(x1,y1,x2,y2):
return x1*y2 - x2*y1
def is_convex(n, vertexes):
#n多角形の判定
flg = True #入力された図形が凸ならTrue/凸でないならFalse
for i in range(n):
#3頂点を時計回りに参照
a = vertexes[i%n]
b = vertexes[(i+1)%n]
c = vertexes[(i+2)%n]
#ベクトルab, bcを計算
vec_ab = [b[0]-a[0], b[1]-a[1]]
vec_bc = [c[0]-b[0], c[1]-b[1]]
#外積が
if cross(*vec_ab, *vec_bc)<0:
flg = False
break
#flg=True の場合は凸多角形、Falseは凸でない多角形
return flg
ただし、vertexesは以下のような形式で与えられるとします。
vertexes = [ [x1, y1], [x2,y2],...,[xn,yn]] #それぞれ頂点1,頂点2,...の座標まとめ
凸多角形の判定方法について原理とpythonコードを紹介しました。参考になれば幸いです。
今回取り上げたpythonコードに関しては、AIZU ONLINE JUDGE にて正解になることを確認しています。
Aizu Online Judge


コメント