最短経路問題を解くアルゴリズムの一つで、すべてのグラフの頂点間の最短経路を見つけることができる。本記事では、
- pythonのコード
- 簡単なグラフに適用した際のアルゴリズムの流れ
の2点をまとめます。特に実行例では、初学者(私を含む)の方にもイメージしやすいよう、各辺への操作を一つ一つ丁寧に取り上げています。
ポイント
- 負の重みを持つグラフにも適用可能
- 負閉路の検出にも適用可能
- 計算量は $O(V^3)$ ($V$ は頂点の個数)
- すべての頂点間の最短経路を計算できる(全点対間最短経路問題)
コード
このアルゴリズムを一言で言うと、『3つの頂点 $i, ,j, k$ を選択し、$k$を経由する経路 $i->k->j$ が 経由しない経路 $i->j$ より小さければ、$i->j$ を更新する』という方法です。
def Warshall_Floid(G):
"""
G: 隣接グラフ
"""
inf = float('INF')
num_nodes = len(G) #頂点数
dist = [[inf]*num_nodes for _ in range(num_nodes)] #テーブルを用意
#テーブルを初期化: 同じ頂点は重み0 かつ 隣接グラフG[From][To]=weight を入力
for frm in range(num_nodes):
dist[frm][frm] = 0 #初期化1 同じ頂点は重み0
for to, weight in G[frm]:
dist[frm][to] = weight
#フロイドワーシャル法のコア部分
for k in range(num_nodes):
for From in range(num_nodes):
for To in range(num_nodes):
if dist[From][k] + dist[k][To] < dist[From][To]:
dist[From][To] = dist[From][k] + dist[k][To]
#負閉路の検出 dist[i][i]<0となる頂点iがあれば負閉路が存在
NEGATIVE_CYCLE = False
for i in range(num_nodes):
if dist[i][i] < 0:
NEGATIVE_CYCLE = True
break
return dist, NEGATIVE_CYCLEアルゴリズムの流れの確認
以下のグラフを用いて、視覚的にアルゴリズムの流れを確認します。

このグラフに対する距離のテーブル dist は以下のようになります。ただし、テーブルの行,列の指定は0はじまりとします。
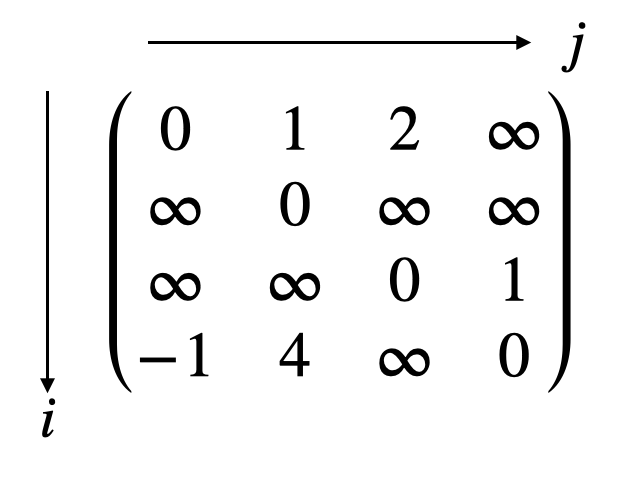
dist$k=0$ の場合
$i \rightarrow 0 \rightarrow j$ の経路を考えます。ただし、$i,j \in \{1,2,3\}$ です。
例えば $i=3$, $j=1$を注目しますと、$dist_{3,1}=4$ です。これに対して、頂点0を経由するルート$3 \rightarrow 0 \rightarrow 1$ は、$dist_{3,0}+dist_{0,1}=-1+1=0$です。
したがって、$dist_{3,1}=4 > dist_{3,0}+dist_{0,1}=0$ が成り立つため、dist は更新されます。
同様に、$i=3$, $j=2$ も $dist_{3,2}=\infty > dist_{3,0}+dist_{0,2}=1$ が成り立つため、 dist は更新されます。その他の組み合わせは $dist_{i,j} \leq dist_{i,0}+dist_{0,j}$のため更新されません。
結果、以下のようなテーブルになります。赤字は更新された数字です。
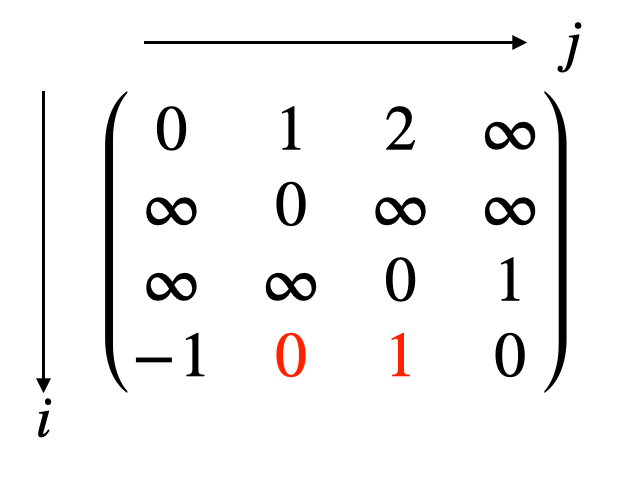
$k=1$ の場合
すべて $dist_{i,j} \leq dist_{i,1}+dist_{1,j}$ となり、更新はありません。
$k=2$ の場合
$i=0$, $j=3$ の場合のみ、 $dist_{0,3}=\infty > dist_{0,2}+dist_{2,3}=3$ となって更新されます。
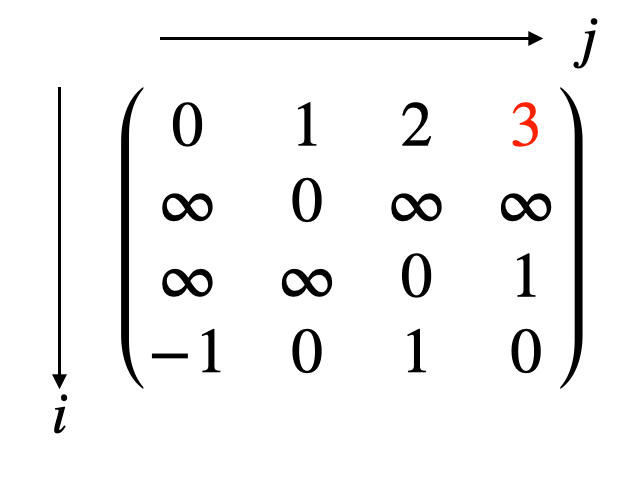
$k=3$ の場合
更新されるのは以下の2つです。
- $i=2$, $j=0$ の場合: $dist_{2,0}=\infty > dist_{2,3}+dist_{3,0}=0$
- $i=2$, $j=1$ の場合: $dist_{2,1}=\infty > dist_{2,3}+dist_{3,1}=1$
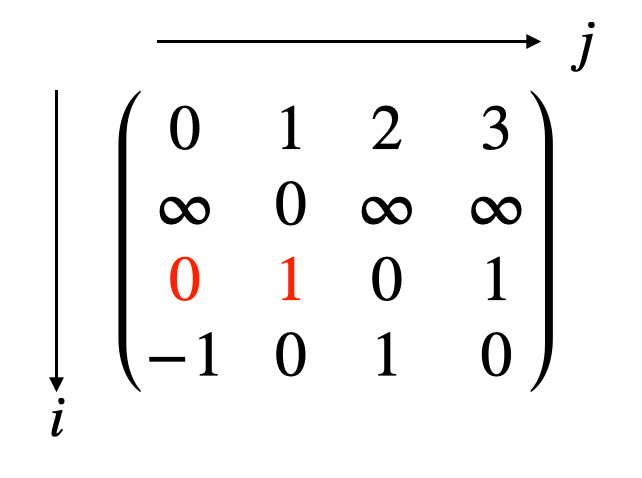
まとめと参考
ワーシャルフロイド法のpythonでの実装と、アルゴリズムの流れをメモしました。
上記のpythonコードは AOJ GRL_1_C で正解になることを確認しています。
最短経路を求める他のアルゴリズム(ベルマンフォード法、ダイクストラ法)については以下の私の記事でも述べています。ご興味があればぜひ。
ベルマンフォード法
ダイクストラ法
記事の執筆には、以下の書籍を参考にしました。
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年




コメント