高校数学の場合の数でよく見る、二次元のグリッドの道順総数を解く問題を扱います。この問題を解くための複数のアルゴリズムを紹介します。
扱う問題と2つの解法
二次元のグリッド上の経路を求める問題です。
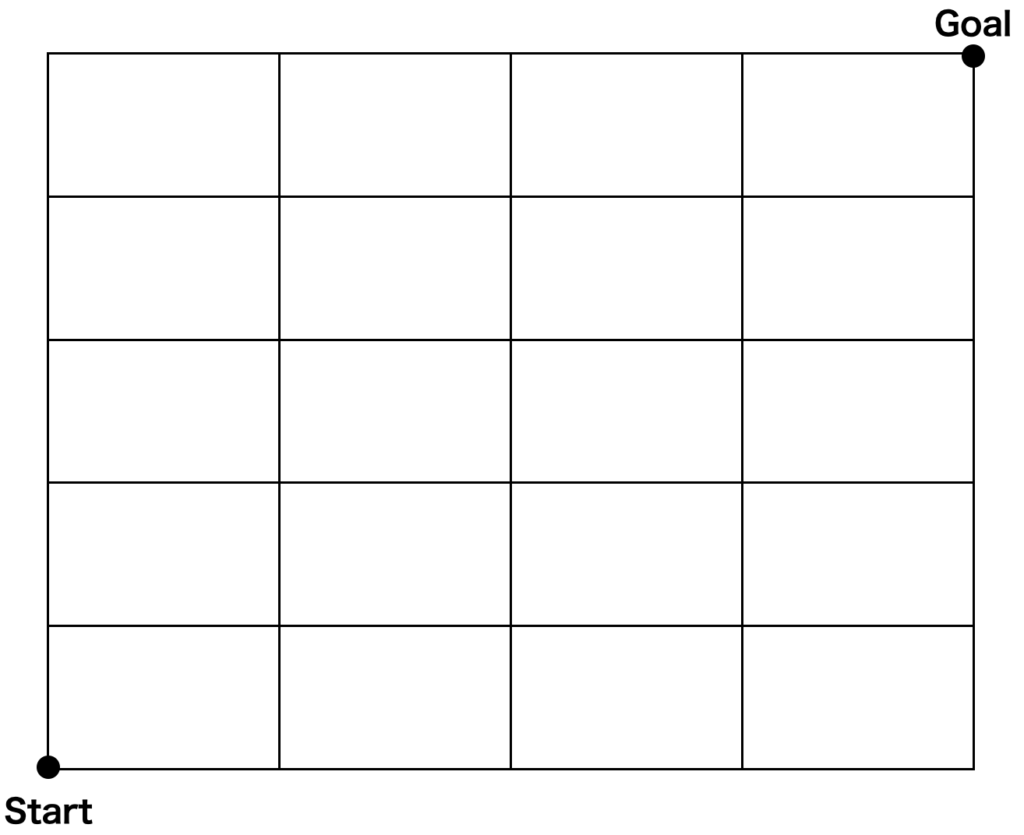
この問題の解法は2種類あります。
- 書き込む方法
- 同じものを含む順列
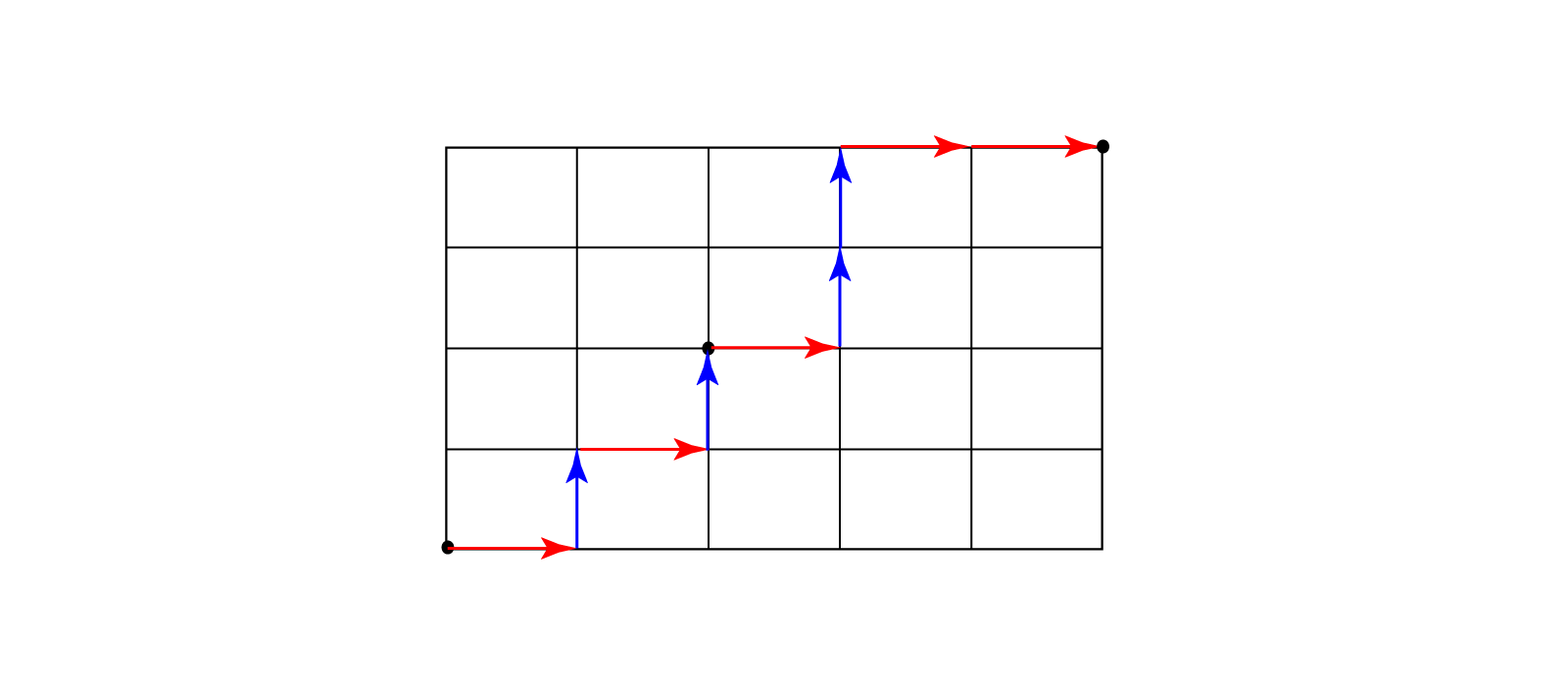
1.の方法では、各点に『その点までの最短経路の本数』を書き込んでいきます。

ある点への最短経路数は、下のマスと左のマスの最短経路数の合計値である事実を使って計算します。
このアイデアは動的計画法に繋がっています。
2.の方法では、下方向に3マス・右方向に4マス通過する必要があります。従って、合計7このうち、どこに↑を3個おき、どこに→を4個置くかと考えれば解くことができます。
$$\frac{7!}{3!4!}=35通り$$
詳細は以下のサイトなどをご参照ください。
扱う問題について
横W x 縦 H のグリッドがあります。左から i 番目、下から j 番目のマス目には (i,j) という番号がついています。
高橋君は、マス目 (i,j) から(i+1,j) または (i,j+1) に進むことができます。高橋君が (1,1) から (W,H) まで行く経路の個数を 1,000,000,007 で割ったあまりを求めてください。
AtCoder Beginner Contest 034 C-経路
$W,H$ はマスの個数ではなく、線の本数であることに注意が必要です。

書き込む方法を使って解く
動的計画法の場合
※100点の解法。上の問題は満点が101点が満点であることに注意。
MOD = 10**9+7
W,H = map(int, input().split())
dp = [[0]*W for _ in range(H)]
dp[0][0] = 1
for h in range(H):
for w in range(W):
if w==0 and h==0:
continue
if w-1 >= 0:
dp[h][w] += dp[h][w-1]
if h-1 >= 0:
dp[h][w] += dp[h-1][w]
dp[h][w] %= MOD
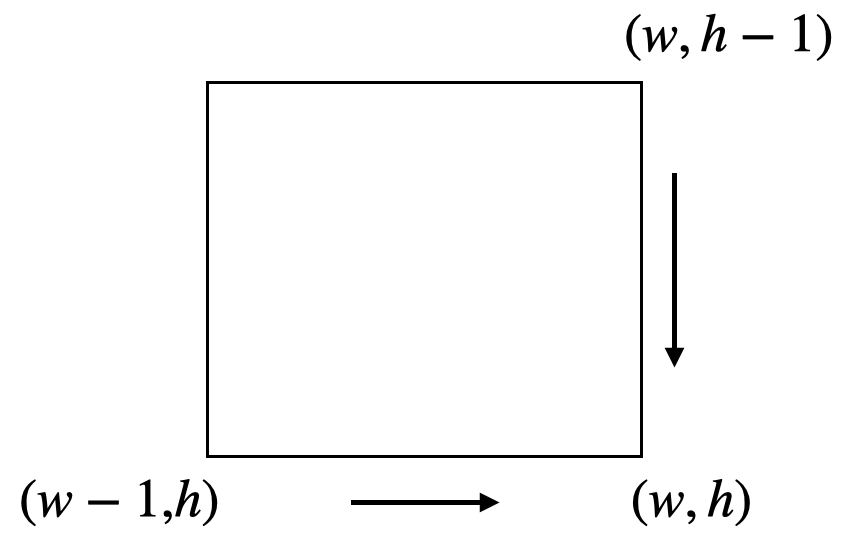
print(dp[-1][-1])書き込む方法と同じ考え方です。ある点$(w,h)$への最短経路数は、1マス上の$(w,h-1)$の最短経路数と1マス左$(w-1, h)$の最短経路数の合計値として計算します。
メモ化再帰の場合
※100点の解法。上の問題は満点が101点が満点であることに注意。
#再帰の上限回数
import sys
sys.setrecursionlimit(10**6)
MOD = 10**9+7
W,H = map(int, input().split())
memo = [[-1]*(H) for _ in range(W)]
def rec(w,h):
#ベースケース
if w<0 or h<0:
return 0
#初期値でない場合、メモの値を返す
if memo[w][h] != -1:
return memo[w][h]
if w==0 and h==0:
memo[w][h] = 1
return memo[w][h]
#漸化式
else:
memo[w][h] = rec(w-1,h) + rec(w,h-1)
memo[w][h] %= MOD
return memo[w][h]
ans = rec(W-1,H-1) #0始まりで数える
print(ans)ゴールからスタート地点へ遡って経路数を数え上げていきます。
基本的なアイデアは動的計画法と同じですが、計算の始点が異なります。動的計画法はスタートからゴールへ計算していますが、上のメモ化再帰ではゴールからスタートへ向かって計算します。
グリッド数は0始まりのため、ゴールの位置は$W,H$ではなく$W-1, H-1$としています。
再帰関数の書き方のコツや考え方について、以下の記事で紹介しています。
同じものを含む順列で解く方法
※101点満点の解法
上方向↑を$H-1$個、右方向→を$W-1$個並べる場合の数を計算します。
よって、以下の計算式をプログラムで解けば良いことになります。
$$\frac{(H+W-2)!}{(H-1)!(W-1)!} = \frac{A}{B}$$
便宜上、分子を$A$、分母を$B$とします。
ただし、$H,W$の階乗は非常に大きな値になりうるため、modの計算について2つの工夫が必要となります。
- $n! \equiv r_0 r_1 … r_n \pmod m$
- $(H-1)!(W-1)!$の逆元
1について
$N=M\cdot k_N+r_N$と書けるため、
$$n! = n\cdot (n-1)\cdot … 1$$
$$=(M\cdot k_{n}+r_n)\cdot (M\cdot k_{n-1}+r_{n-1})… (M\cdot k_1 + r_1)$$
よって、 $M\cdot k_i$の部分は$M$で割った余りが0のため、1.の式が導出されます。
2について
求めたい値は$A \times B^{-1} \pmod M$であるため、$B^{-1}$を$M$で割った余りを求める必要があります。それを逆元といいます。
求めるにはフェルマーの小定理を利用します。$p$を素数として、
$$a^p \equiv 1\pmod p$$
が成り立ちます。これを変形して、
$$a^{p-2} \equiv a^{-1} \pmod p$$
これより、$B^{-1} \pmod M$の計算の代わりに、$B^{M-2}\pmod M$を掛け算すれば良いと考えることができます。
MOD = 10**9+7
W,H = map(int, input().split())
#分子のmod計算
A = 1
for i in range(1, H+W-2+1):
A *= i
A %= MOD
#分母のmod計算
B = 1
for i in range(1, H-1 +1):
B *= i
B %= MOD
for i in range(1, W-1 +1):
B *= i
B %= MOD
#逆元を利用
ans = (A*pow(B, MOD-2, MOD))%MOD
print(ans)まとめ
グリッド上での最短経路数の数え上げ方法についてまとめました。
問題自体は高校数学の典型問題ですが、プログラムではいろいろな解き方があって興味深いです。
参考になれば幸いです。
逆元については、以下のサイトなどをご覧ください。

フェルマーの小定理