本記事では、
- 最大フローとは何か
- 最大フローを求めるアルゴリズム
- 簡単なグラフを例に、どのようにアルゴリズムが進んでいくかのデモ
の3点がわかるように解説していきます。
最大フロー(最大流)とは何か
まずはフローの意味から解説します。
フロー(flow)は『流れ』を意味する英単語であり、この問題においては
頂点sから頂点tへ”移動するもの”
という意味で解釈できます。
“移動するもの”の例として、水の流れる量や物資の運搬量などが挙げられます。
“移動するもの”はグラフを自由に移動できる訳ではなく、各辺に通過できる量の上限が設定されています。この値を容量と呼び、各辺の容量以上は通過できないという制限がつけられています。
ちなみに、最大フロー問題では、各辺に “(フローの量)/(容量)” という形式で設定が書かれていることが多いです。
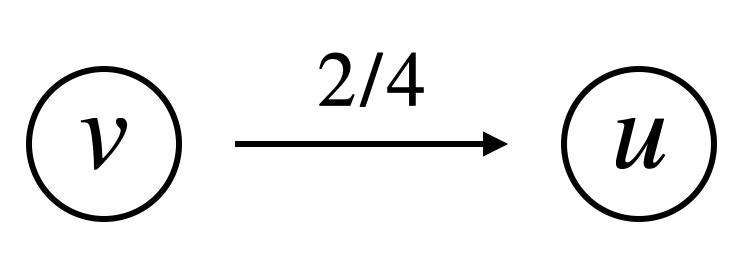
以上を踏まえ、最大フロー(最大流)問題とは以下の問題と定義できます。
各辺の上限を越えずに、頂点sから頂点tへものを移動させる時の最大量はいくらか?
アルゴリズムの準備: 残余グラフについて
上記で述べた最大フロー(最大流)問題を解くためのアルゴリズムとして、フォード・ファルカーソン法が挙げられます。このアルゴリズムを理解するためには、残余グラフの概念を知っておくが重要です。
残余グラフ
残余グラフを一言で言うと、各辺(有向辺)に逆向きの辺を設置したグラフ のことを意味します。この逆向きの辺のことを逆辺と呼びます。
この残余グラフの重要な性質として、逆辺のフローは辺に流れるフローと同じ量になる という点です。
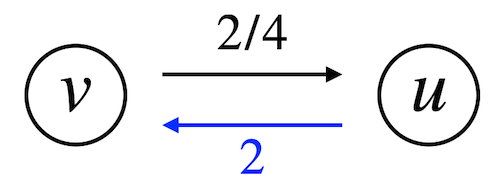
初期状態では、全辺のフローが0のため、逆辺の容量も0に設定されています。そして、この辺に流したフローの量の分だけ、逆辺の容量も増加します。
残余グラフの実装コードについて
残余グラフには辺とその逆辺が重要であり、辺・逆辺を実装するコードが以下になります。
G = [[] for _ in range(V)] #隣接グラフ
#逆辺も考慮した辺の初期化
def add_edge(From, To, c):
#len(G[v])は逆辺を取得するための手がかり
G[From].append([To, c, len(G[To])]) #辺の追加(終点ノード, 容量, 逆辺のインデックス)
G[To].append([From, 0, len(G[From]) - 1]) #逆辺の追加From が始点、To が終点の辺です。これらを隣接グラフに追加する関数が add_edge() 関数です。
G[From] に追加されるリストのうち、第一項目は終点ノード、第二項目は容量、第三項目は逆辺を指定する番号です。
全ての要素は隣接グラフ G[From], G[To] に後ろから追加されていくため、appendする直前のG[From], G[To] の要素数が分かれば逆辺を特定可能です。
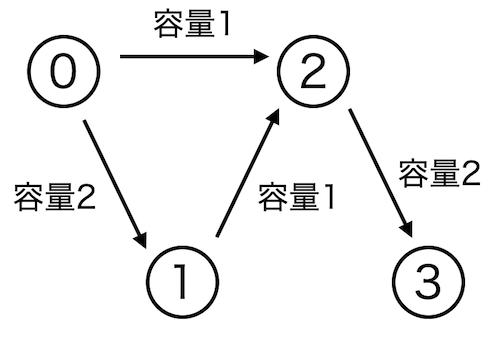
例として以下の隣接グラフを考えます。
G = [[[1, 2, 0]], [[0, 0, 0], [2, 1, 0]], [[1, 0, 1]]]このうち、ノード0の要素をみてみます。
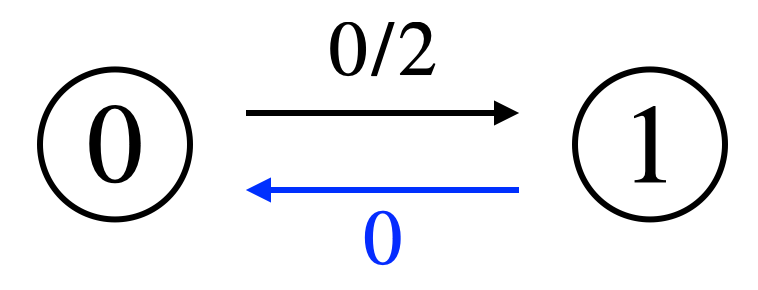
G[0][0] = [[1, 2, 0]]これは、ノード0はノード1へ容量2の辺を持っており、この逆辺はG[1]の0番目の要素であることを意味しています。 G[1]の0番目 を確認すると、
G[1][0] = [0, 0, 0]ノード1がノード0へ容量0の有向辺を持っており、この逆辺はG[0]の0番目の要素であることを意味しており、辺・逆辺の対応が取れていることがわかります。
最大フローを求めるアルゴリズムコード
これを踏まえて、最大フローを求めるアルゴリズムをpythonで実装します。
実装には、以下の4つの関数を作成します。
add_edge(): 辺と逆辺を設定bfs(): 幅優先探索 (始点sから各ノードへの距離を計算)dfs(): 深さ優先探索 (残余グラフ上でs-tパスの探索を実行)get_maxflow(): s-tパスの最大フローを求める
#max_flow.py
from collections import deque
#逆辺も考慮した辺の初期化
def add_edge(u, v, c):
#len(G[v])は何を意味してる?->逆辺を取得するための手がかり
G[u].append([v, c, len(G[v])])
G[v].append([u, 0, len(G[u]) - 1])
#sからの最短距離を計算する
def bfs(s):
#D: sからの距離を管理
D = [-1] * V
D[s] = 0
Q = deque()
Q.append(s)
while len(Q) > 0:
v = Q.popleft()
for next, capa, _ in G[v]:
if capa > 0 and D[next] < 0:
D[next] = D[v] + 1
Q.append(next)
return D
#増加パス: すでに存在するs-tパスと共有する辺は逆流を許して
# 新たに追加できるs-tパスのこと
#2頂点s-t間の辺連結度を求める
#深さ優先探索(v始点, tゴール, f流量, D距離リスト)
##seen[v]: vから出る辺のうち、チェックした個数
def dfs(v, t, f, seen, D):
if v == t:
return f
#頂点vから出る(逆辺も含む)辺を全て探索
while seen[v] < len(G[v]):
next, capacity, rev = G[v][seen[v]]
#流す余地があり、かつ始点から遠ざかる方向のノードであれば探索
if capacity > 0 and D[v] < D[next]:
#min(f,capacity)は、s-tパスのうち最小容量しか流すことができない
#ため必要になる
flow = dfs(next, t, min(f, capacity), seen, D)
if flow > 0:
G[v][seen[v]][1] -= flow #flow分流せる流量が減る
G[next][rev][1] += flow #逆流分足される
return flow
#探索ノード数
seen[v] += 1
return 0
def calc_max_flow(s, t):
flow = 0
while True:
D = bfs(s)
if D[t] < 0:
return flow
#頂点vから出るパスのうち、チェックした個数を管理
seen = [0] * V
while True:
f = dfs(s, t, 1e10, seen, D)
if f == 0:
break
flow += f
if __name__=="__main__":
V, E = map(int, input().split())
G = [[] for _ in range(V)]
for _ in range(E):
u, v, c = map(int, input().split())
add_edge(u, v, c)
max_flow = calc_max_flow(0, V - 1) #始点0, 終点V-1ノードの最大フロー
print(max_flow)幅優先探索では始点sから各ノードへの距離を探索し、リスト D で管理します。
深さ優先探索(dfs)では、再帰関数を用いて始点sから終端tまでの経路を探索し、その経路に流すことができるフローの量を計算します。
# v: 今いるノード
# t: ゴールのノード
# f: 今まで流したフロー、
#seen: ノードvから出ているパスのうち、チェックした個数を管理するリスト
#D: 幅優先探索で得られた、始点sからの距離を管理するリスト
def dfs(v, t, f, seen, D):
...略...以下のコードのように各辺・逆辺の容量を更新する部分が最大フロー問題に特有な部分です。
#s-tパスのフローが確定した後、容量を更新
if flow > 0:
G[v][seen[v]][1] -= flow #flow分流せる流量が減る
G[next][rev][1] += flow #逆流分足される
return flowアルゴリズムのデモ

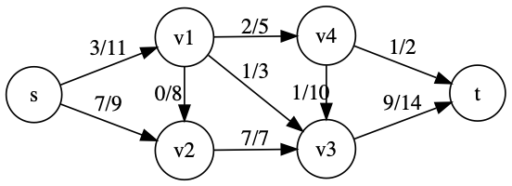
図2のグラフを用いて、頂点0から頂点3への最大フローを求めてみます。わかりやすさのため、map() 関数は用いずに直接入力しています。
#max_flow.py
#...略...
if __name__=="__main__":
V, E = 4, 4 #頂点数, 辺の本数
G = [[] for _ in range(V)]
es = [[0, 1, 2], [0, 2, 1], [1, 2, 1], [2, 3, 2]] #このグラフの辺のリスト
for _ in range(E):
u, v, c = map(int, input().split())
add_edge(u, v, c)
max_flow = calc_max_flow(0, V - 1) #始点0, 終点V-1ノードの最大フロー
print(f"最大流は {max_flow}")
#最大流は 2このように最大流の問題を解くことができます。
アルゴリズムの動作の流れを一つ一つ可視化
次に上記のアルゴリズムを図5のテストグラフに適用し、プログラムの挙動を一つ一つ丁寧に見ていきます。このグラフを解くまでに、幅優先探索 bfs()関数 で距離リストの更新が 3回 行われます。
そこで、アルゴリズムの流れをbfs()関数の更新のタイミングで区切って見ていきます。
#図5の隣接グラフG
#G = [[[1, 2, 0], [2, 1, 0]], [[0, 0, 0], [2, 1, 1]], [[0, 0, 1], [1, 0, 1], [3, 2, 0]], [[2, 0, 2]]]
max_flow = calc_max_flow(0, 3) #始点0, 終点V-1ノードの最大フロー幅優先探索 1回目の実行
#calc_max_flowの中(56行目)
while True:
D = bfs(s)
#D = [0,1,1,2]1回目の幅優先探索で、始点0から各ノードへの距離を計算します。この距離リスト D を用いて深さ優先探索 dfs() を計算します。
まずは始点0からの探索を実行します。
f = dfs(v=0, t=3, f=1e10, seen=[0,0,0,0], D=[0,1,1,2])始点0からの探索 1
37行目以下の while文 内を見ていきます。リストの深さは再帰関数の深さとします。
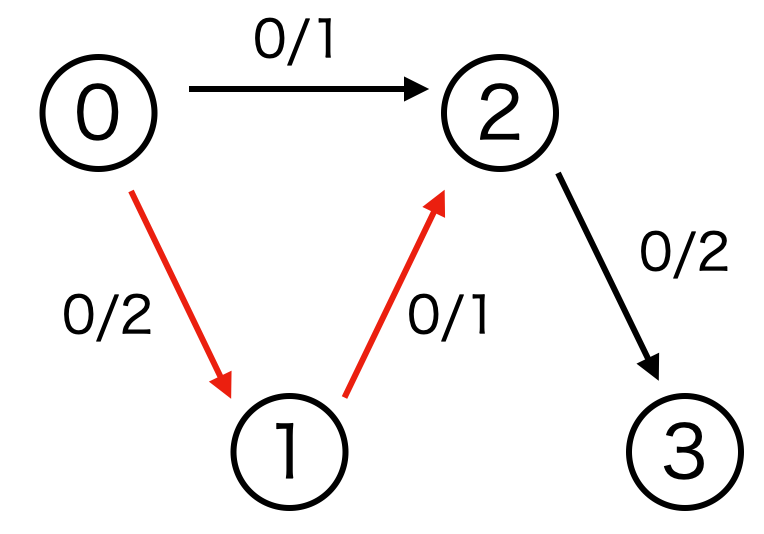
next, capacity, rev = 1,1,0のとき: capacity >0 and D[0]<D[1]より、43行目のif文に入るf = dfs(v=1, t=3, f=1, seen, D)を計算next, capacity, rev = 0,0,0:D[v=1]$\nless$D[next=0]より終了next, capacity, rev = 2,1,1:D[v=1]$\nless$D[next=2]より終了
- ここで
v=1の探索は終了
ここまでの流れは、0→1->2の経路 (赤線) を探索したことになります。
始点0からの探索 2
再び37行目以下の while文 内を見ていきます。次は頂点2を探索します。リストの深さは再帰関数の深さとします。
next, capacity, rev = 2,1,0のとき:capacity >0 and D[0]<D[2]より、43行目のif文に入るf = dfs(v=2, t=3, f=1, seen, D)を計算next, capacity, rev = 0,0,0:D[v=2]$\nless$D[next=0]より終了next, capacity, rev = 2,1,1:D[v=2]$\nless$D[next=2]より終了next, capacity, rev = 3,2,0:D[v=2]<D[next=3]より46行目に入るf = dfs(v=3, t=3, f=1, seen, D)を計算(46行目)v=t=3より、flow=1に確定
- 経路2→3の辺・逆辺のフローを更新(48,49行目)
G[2][3][1] = 2 - 1 = 1(辺のフローを更新)G[3][2][1] = 1(逆辺のフローを更新)
- 経路0→2 の辺・逆辺のフローを更新(48,49行目)
G[0][2][1] = 1 - 1 = 0(辺のフローを更新)G[2][0][1] = 1(逆辺のフローを更新)
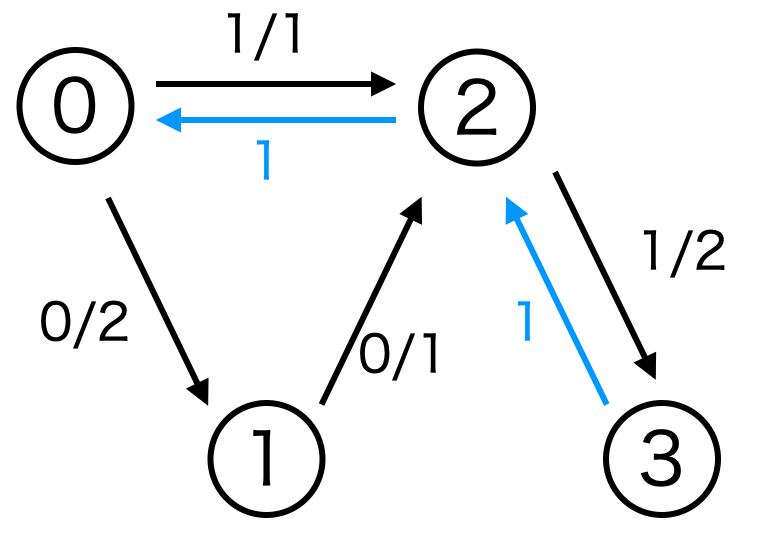
ここまでの流れは 0→2→3 の経路を探索したことになります。(赤線)

これまでの結果、残余グラフは以下のように更新されました。
幅優先探索 2回目の実行
図6-3に対して幅優先探索を実行します。
while True:
D = bfs(s)
#D = [0,1,2,3]ノード0からノード2 までの辺はこれ以上フローを流せないため、直接通行することができません。それにより 0→1→2 を経由する必要があるため、 D[2]=2 となっています。
始点0からの探索を行います。
f = dfs(v=0, t=3, f=1e10, seen=[0,0,0,0], D=[0,1,2,3])始点0からの探索 1
37行目以下の while文 内を見ていきます。リストの深さは再帰関数の深さとします。
next, capacity, rev = 1,1,0のとき:capacity >0 and D[0]<D[1]より、43行目のif文に入るf = dfs(v=1, t=3, f=1, seen, D)を計算next, capacity, rev = 0,0,0:D[v=1]$\nless$D[next=0] より終了next, capacity, rev = 2,1,1:D[v=1]<D[next=2]より46行目に入るf = dfs(v=2, t=3, f=1, seen, D)を計算(46行目)next = 0:D[v=2]$\nless$D[next=0]より終了next = 1:D[v=2]$\nless$D[next=1]より終了next = 3:D[v=2]<D[next=3]より46行目に入るf = dfs(v=3, t=3, f=1, seen, D)を計算(46行目)v=t=3より、flow=1に確定
- 経路2→3の辺・逆辺のフローを更新(48,49行目)
G[2][3][1] = 1 - 1 = 0(辺のフローを更新)G[3][2][1] = 1+1= 2(逆辺のフローを更新)
- 経路1→2 の辺・逆辺のフローを更新(48,49行目)
G[1][2][1] = 1 - 1 = 0(辺のフローを更新)G[2][1][1] = 1(逆辺のフローを更新)
- 経路0→1 の辺・逆辺のフローを更新(48,49行目)
G[0][1][1] = 2 - 1 = 0(辺のフローを更新)G[1][0][1] = 1(逆辺のフローを更新)
これまでの流れは、以下の赤線の部分を探索したことを意味します。

この結果、残余グラフは以下のように更新されました。

幅優先探索 3回目の実行
図6-5の残余グラフに対して幅優先探索を実行します。
while True:
D = bfs(s)
#D = [0,1,-1,-1]終点ノード 3 到達できない(D[3]=-1) ため、ここで探索が終了します。到達できない理由は、頂点0→頂点1の辺以外、容量と同じ量のフローが通過済みであるためです。
まとめ
最大フロー問題についてのアルゴリズムを解説し、その挙動を簡単なグラフを用いて丁寧に追っていきました。ちなみに、最大流問題を解くアルゴリズムのことをフォードファルカーソン法と呼びます。
今回紹介したコードは AIZU ONLINE JUDGE 6_A で正答になることを確認しています。
今回のアルゴリズムでは、グラフ探索に関する重要アルゴリズム(幅優先探索・深さ優先探索・残余グラフ)を組み合わせて解く必要があります。以下の書籍に詳細に書かれているので、理解が曖昧な方はぜひ確認してみてください。
参考図書
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年

コメント