k-menas法はデータ点の距離の近さを基準にk個のクラスタに分割する手法です。このアルゴリズムの改良版がk-menas++です。
はじめに
k-means法とk-means++のの手法の違いは、データの初期化方法です。
k-means法については私の過去のページでも紹介していますので,よろしければご覧ください。
k-means法の問題点
k-means法では、クラスタの初期重心を求める際に乱数を振って決めています。そのため、同じデータ点を対象にしても、クラスタ結果が以下のように変わってしまう場合があります。
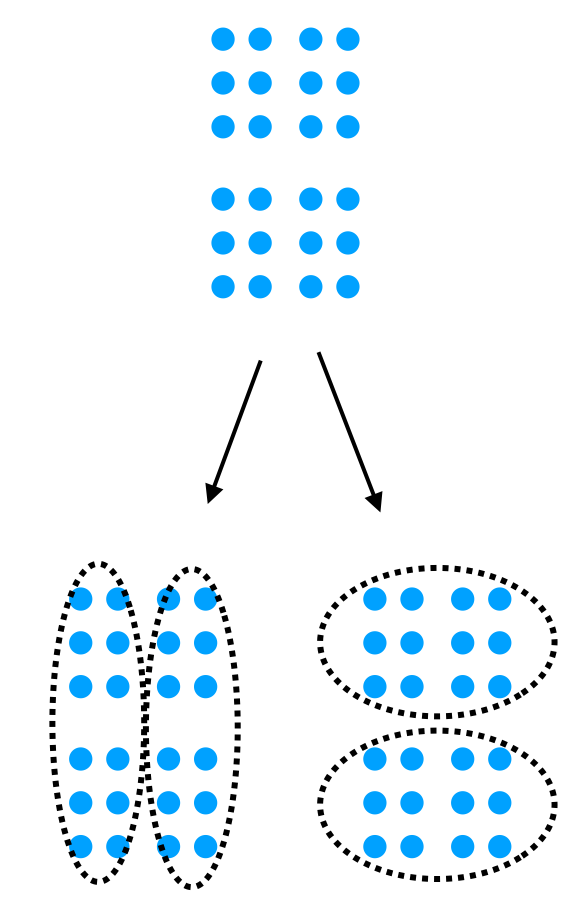
しかしながら、以下の2つの結果を評価する明確な指標がなく、どっちを採用すべきか判断するのが難しいという問題があります。
k-means++について
上記のk-means法の初期値依存を改善する手法として提案されたのがk-means++[2]です。基本的なアイデアは、『初期の中心点をなるべく遠くにする』です。
k-means++では、以下のように距離を変数に持つ確率分布を用いて初期重心を選択します。
$$\frac{D(x_i)}{\sum_j D(x_j)}$$
この確率分布の分子は点$i$と重心との最短距離で、分母は各点と中心との最短距離の総和です。この確率分布を平たく言えば、『遠い点ほど高い確率で中心に選ばれる』ということです。
距離にしたがって確率的に中心を選択できることの利点は、外れ値への頑強性が高くなるということが挙げられます。最遠方の点を選択する方法だと、外れ値が選択される場面が多くなるという問題が発生します。
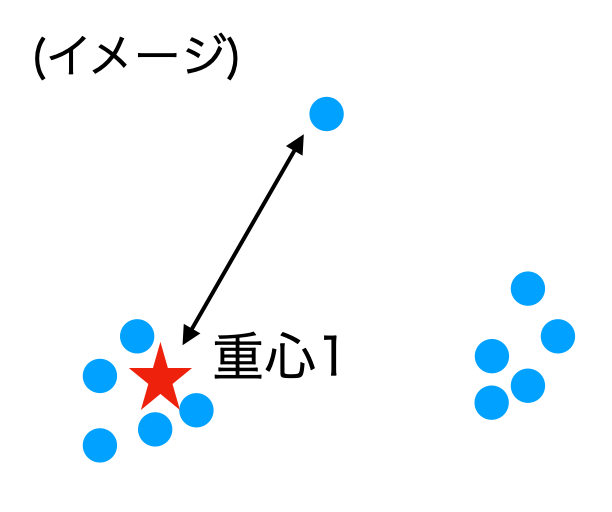
ちなみに、距離が一番遠いものを選んでいくという初期化方法(Katsavounidis 1994)も提案されており、kmeans++はこの手法の改良版のようです。
k-means++のアルゴリズム
- データ点の集合から、1点をクラスタ中心としてランダムに選択
- あるデータ点 $i$ と各々のクラスタ中心との距離を計算し、最も近いものを $D(x_i)$ と定義する。この操作を全データに対して実行する
- $D(x_i)/\sum(D(x_j))$ の確率分布にしたがって、データ点を1点選択してクラスタ中心とする。
- $k$ 個のクラスタ中心を得られるまで2., 3.の計算を繰り返す。
上記のアルゴリズムをpythonで実装したコードが以下になります。
def init(k,X_):
#=======
#k: クラスタ数
#X_ : データ点の座標を格納したnp.array
#=======
clusters = [] #初期重心を管理するリスト
#1. データから一点を選択
centroid_id = np.random.choice([i for i in range(len(X_))])
clusters.append(X_[centroid_id])
X_ = np.delete(X_, centroid_id, axis=0) #選択した点を入力データのリストから除外
# 4. k 個のクラスタ中心を得られるまで計算を繰り返す。
while len(clusters) < k:
dists = []
#2. 各データ点 と各クラスタ中心との距離を計算し、最も近いものを取り出す
for x_i in range(len(X_)):
dist = float('INF')
for cent_j in range(len(clusters)):
dist = min(dist, distance(X_[x_i], clusters[cent_j]) ) #今まで見た最短距離と今見てる距離との小さい方を選択
dists.append(dist)
len_dist = len(dists)
#3. 確率分布にしたがって、データ点を1点選択してクラスタ中心とする。
prob = dists / np.sum(dists) #確率分布
new_c = np.random.choice([i for i in range(len_dist)], p=prob) #確率分布から点を一点取り出す
clusters.append(X_[new_c])
X_ = np.delete(X_, new_c, axis=0) #取り出した要素を消去
#距離のリストを初期化
dists = []
return clustersちなみに、初期化後の計算は k-means と同じ手順でクラスタリングされます。
自作コードとsklearnとの比較
k-means++の初期化のアルゴリズムをsklearnの手法と比較します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.cluster import kmeans_plusplus
import copy
np.random.seed(16)テストデータは以下の通りです.データ点数1000点、2次元でクラスタ中心は3つで設定しました。
X_, _ = make_blobs(1000, 2,centers=3, random_state=10, cluster_std=1, center_box=(-20,20))
plt.scatter(X_[:,0], X_[:,1])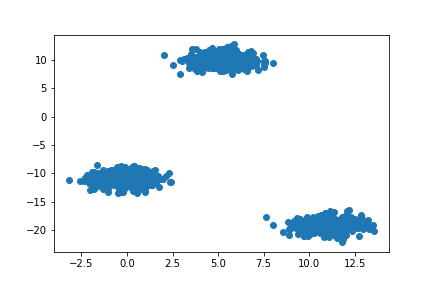
自作コードの実行
#自作コード
centers = init(k, X_)
plt.scatter(X_[:,0], X_[:,1]) #データ点の散布図
for i in range(k):
c = centers[i]
#print(type(c), c)
plt.scatter(c[0], c[1], label=f'{i}', marker="X", s=100) #初期重心の位置
plt.legend()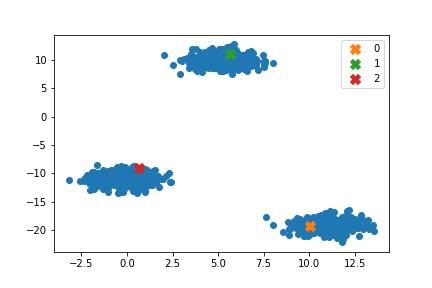
sklearnの結果
sklearnでは複数回重心を求め、最も良い場合を選択するようになっています。今回は自作コードとの比較が主目的のため、kmeans_plusplusの引数$n_local_trials=1$に設定しています。
#sklearn
centers_sk, _ = kmeans_plusplus(X, n_clusters=k, n_local_trials=1)
plt.scatter(X[:,0], X[:,1])
for i in range(k):
c = centers_sk[i]
print(type(c), c)
plt.scatter(c[0], c[1], label=f'{i}', marker="X", s=100)
plt.legend()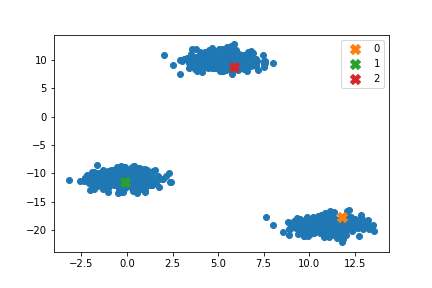
sklearnと矛盾しない結果を得ることができました。
まとめ・参考
k-means++に関して調べ、理解を深めるためにアルゴリズムを実装しました。この手法の心は『初期重心同士の距離をなるべく大きく設定する』です。
k-means法との違いは初期化にあり、k-means法ではランダムに初期重心を決めたのに対し、k-means++では距離に応じて確率的に初期重心を選択することが可能となります。
調査に関し、以下の文献・サイトを参考にしました。
[2]“k-means++: The advantages of careful seeding” Arthur, David, and Sergei Vassilvitskii, Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, Society for Industrial and Applied Mathematics (2007)


コメント