転倒数について

2022.08.23
記事内に広告が含まれています。

ある数列において、昇順になっていない数字の組みの数のことを転倒数とよびます。

本記事では、

  • 転倒数の定義と具体例
  • 転倒数を求めるアルゴリズム(バブルソート, BIT)
  • BITを用いた方法の視覚的解釈
  • BITを用いた方法の数式的解釈

についてまとめていきたいと思います。

転倒数の定義と具体例

転倒数の定義は以下になります。

{\text{inv}}(A)=\#\{(A_{i},A_{j})\mid i<j{\text{ and }}A_{i}>A_{j}\}”></p><p></p><cite><a rel=転倒 (数学)- wikipedia

この定義を簡単に言えば、『右側にあるのに自分より小さい数値が何個あるか』ということです。

例えば、数列 $\{4, 3, 2, 1\}$ の転倒数は、$(4,3), (4,2), (4,1), (3,2), (3,1), (2,1)$ の合計 6個 となります。

また、転倒数は昇順にソートされた数列と線で結んだ際の交点の個数としても求められるそうです。

図1: 転倒数の視覚的な計算方法. 赤点の個数が転倒数と一致する

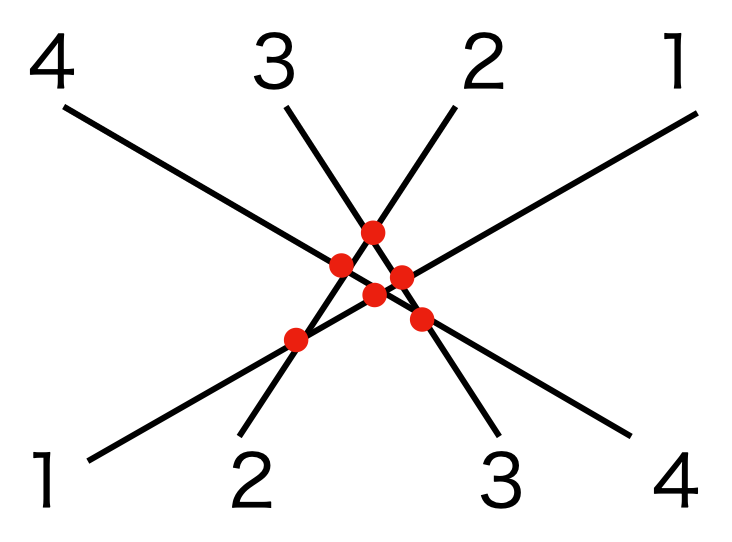
転倒数を求めるアルゴリズム1: バブルソート

バブルソートで交換した数字の個数を計算することで転倒数を求めることが可能です。

def InversionNumberByBubleSort(A):
    ans = []  #転倒数
    for i in range(len(A)):
        for j in range(len(A) - i - 1):
            #左側の方が小さい場合
            if A[j] > A[j + 1]:
                ans.append((A[j], A[j+1]))
                A[j], A[j + 1] = A[j + 1], A[j]
    
    return ans

例えば、数列 $\{4, 3, 2, 1\}$ をバブルソートする際に交換した数字の組みをみると、転倒数 $(4,3), (4,2), (4,1), (3,2), (3,1), (2,1)$ に一致します。

A = [4,3,2,1]
ans = InversionNumberByBubleSort(A)
print(ans)
#[(4, 3), (4, 2), (4, 1), (3, 2), (3, 1), (2, 1)]

計算量は $O(N^2)$ です。

転倒数を求めるアルゴリズム2: BIT

次の方法は、Binary Indexed Tree (BIT) というデータ構造を用いる方法です。

このデータ構造の詳細は私の過去の記事でも紹介しております。ご興味があれば是非ご覧ください。

このアルゴリズムを用いると、転倒数を $O(N \mathrm{log} \ N)$で求められます。

class BIT:

    #初期化
    def __init__(self, n):
        self.size=n
        self.tree = [0] * (n+1) #1-indexのリストで管理
    
    #加算
    def add(self, i,x):
        while i <= self.size:
            self.tree[i] += x
            i += i & -i       #LSBの計算
    #インデックス0からiまでの総和を計算
    def sum(self, i):
        total = 0
        while i >0:
            total += self.tree[i]
            i -= i & -i       #LSBの計算
        
        return total

このコードを利用して、以下のコードで転倒数を求めることができます。

def InversionNumberByBIT(A):
    ans = 0
    Bit = BIT(len(A)) #Binary Indexed Tree
    for i in range(len(A)):
        ans += i - Bit.sum(A[i])
        Bit.add(A[i], 1) #自分の位置を1にする
    return ans

以上のコードを利用し、 数列 $\{4, 3, 2, 1\}$ の転倒数は以下のように求められます。

A = [4, 3, 2, 1]
ans = InversionNumberByBIT(A)
print(ans)
#6

以下では、BITを用いた解法について、視覚的な解釈・数式的な解釈の両方から考えていきたいと思います。

コードの視覚的な解釈

まず前提として、BITはある数字が 0(未出現)か1(既出)か を管理しています。例えば、

Bit.add(A[0], 1) #-> BIT=[0,0,0,1] (A[0]=4 番目に1を設置)

であれば、BIT=[0,0,0,1] となります。ただし、1-indexで考えています。

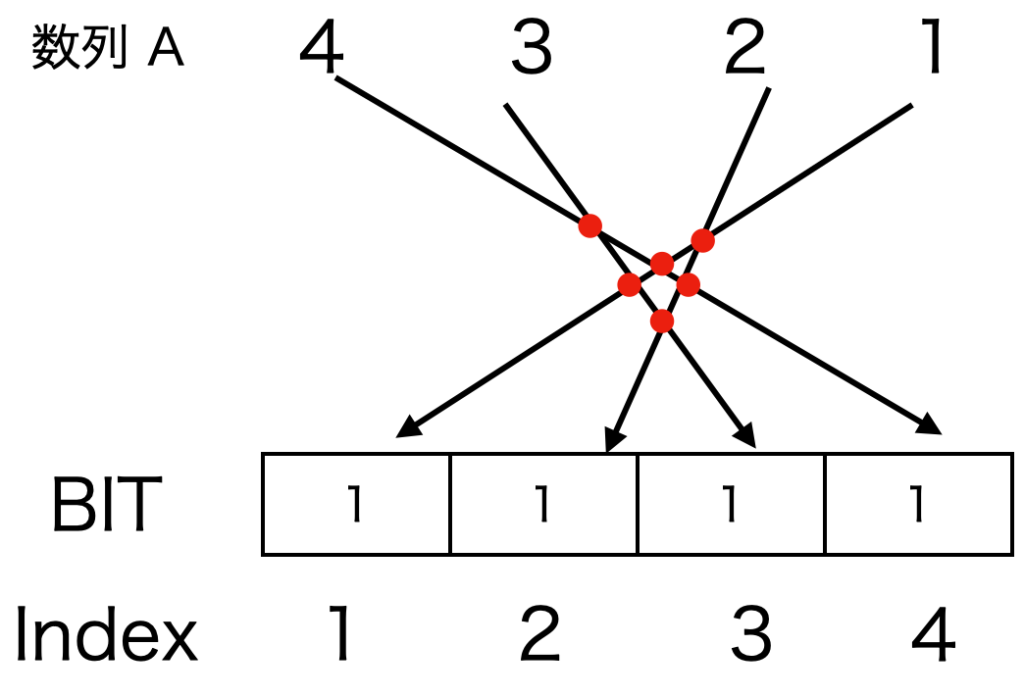
このアルゴリズムは、図1の転倒数と線の交点数が一致することを念頭にコードの流れを考えるとわかりやすいと思います。

$i=0$のとき

$A[0]=4$ をBITに格納するイメージは図2となります。この際、黒線との交点は0個のため、転倒数は0のままになります。

図2: $A[0]=4$の場合. 上が入力した数列 $A$で、下がBITです。

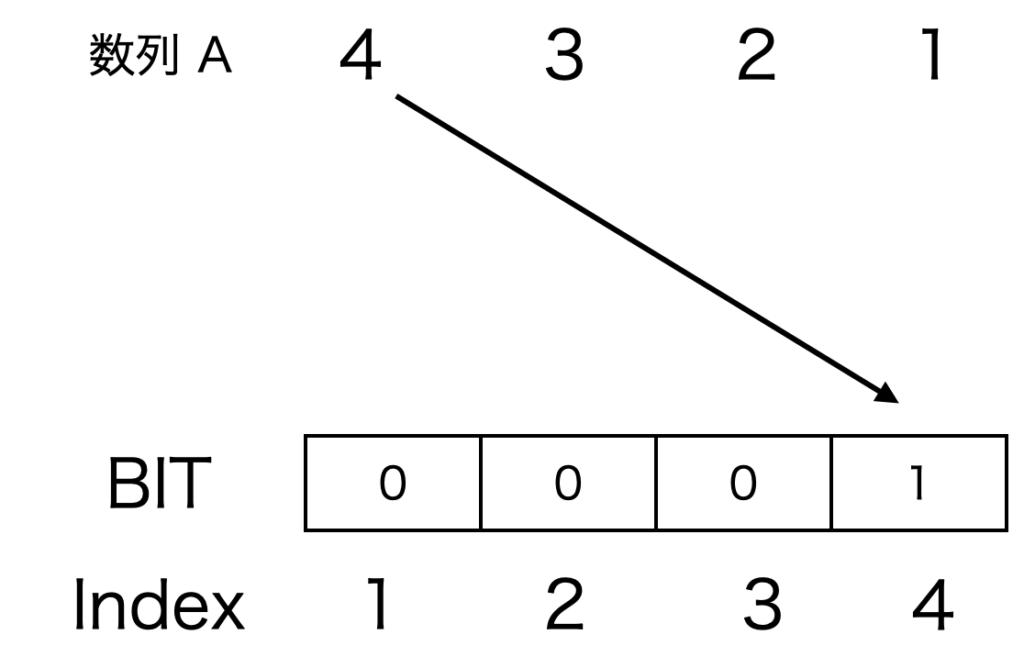
$i=1$のとき

$A[1]=3$ をBITに格納するイメージは図3となります。この際、黒線との交点は1個のため、転倒数は1に更新されます。

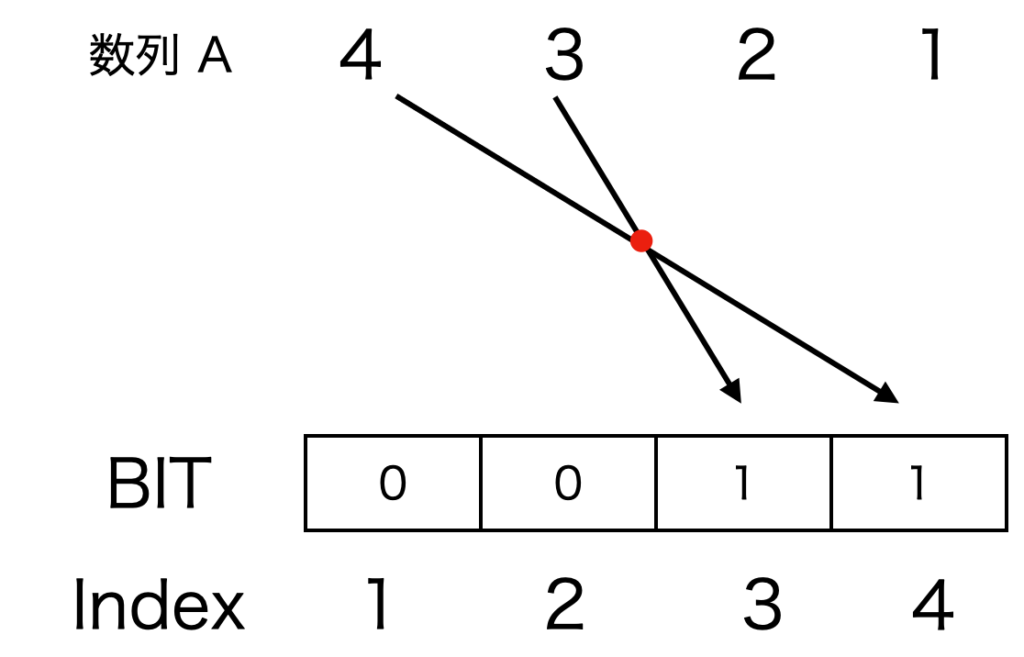
図3 $i=1$ の場合. 赤点が交点を意味する。赤点が1個のため、転倒数が1追加される。

$i=2$のとき

$A[2]=2$ をBITに格納するイメージは図4となります。この際、黒線との交点は2個のため、転倒数は3に更新されます。

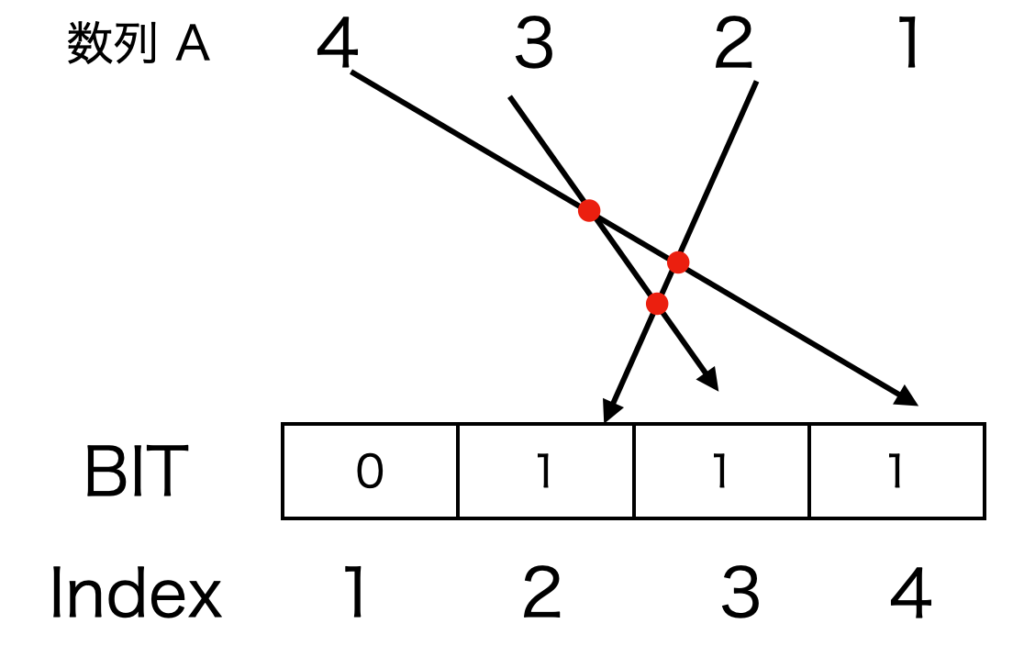
図4: $i=2$の場合。 $A[2]=2$から伸びる矢印は他の2本の矢印と交点を持つため、転倒数は2追加される。

$i=3$のとき

$A[3]=1$ をBITに格納するイメージは図5となります。この際、黒線との交点は3個のため、転倒数は6に更新されます。

図5: $i=3$の場合。$A[3]=1$ から伸びる矢印は他の3本の矢印と交点を持つため、転倒数は3追加される。

コードの数式の解釈

ans += i - Bit.sum(A[i]) について、

右辺第一項目 $i$ はBITに存在する1(既出の数値)の個数、右辺第二項は BITの$A[i]$ よりも左側にある1の個数であると解釈できます。

すなわち、

(今までBITに移動させた数値の個数) – (自分 ($A[i]$) よりも小さい数値の個数) = (自分 ($A[i]$) よりも大きい数値の個数)

を計算していると考えることができます。

右辺の(自分よりも大きい数値の個数) は転倒数そのものなので、BITのコードで転倒数を解くことができます。

まとめと参考

転倒数について、概要とアルゴリズムについてまとめました。また、BITを用いた方法をできる限り噛み砕いてみました。

BITに関しては自分の過去の記事でも触れているので、ご興味があればご覧ください。

BIT(Binary Indexed Tree)をpythonで実装する
Binary Indxed Tree(BIT)は値の追加・区間和を高速に計算できるデータ構造です。 BITをpythonで実装し、アルゴリズムの挙動を一つ一つ詳しく見ていきます。
output-zakki.com
2022.08.20

参考にしたサイトについて

BITを用いた転倒数（反転数）O(N logN)-perogram : 転倒数が昇順にソート列と線で結んだ際の交点数と一致するということを述べていたサイトでした。

転倒数とは – 個人的な競プロメモ : BITのアルゴリズムが転倒数をどう解いているかを噛み砕いて説明してくれている、わかりやすい記事でした。

また、BITは以下の書籍でも取り上げられています。

『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年

コメント