ある整数$x$について、$x^n$を高速に計算する方法(繰り返し二乗法)についてまとめます。
繰り返し二乗法の理解には、2進数とビット演算(特に論理積と右シフト演算)の理解が重要です。
本記事では2進数と論理積、および右シフト演算を簡単に触れ、pythonコードと計算の流れを見ていきます。
目標
- 繰り返し二乗法を要素分解し、一つ一つ理解する
- 繰り返し二乗法のコードの具体的な流れを理解する
アルゴリズムの準備: 2進数、論理積、シフト演算
繰り返し二乗法を理解する上で、以下の3つの項目を理解しておく必要があります。
1. 2進数と10進数の変換
10進数から2進数への変換のポイントは、2で割る操作を繰り返すことです。
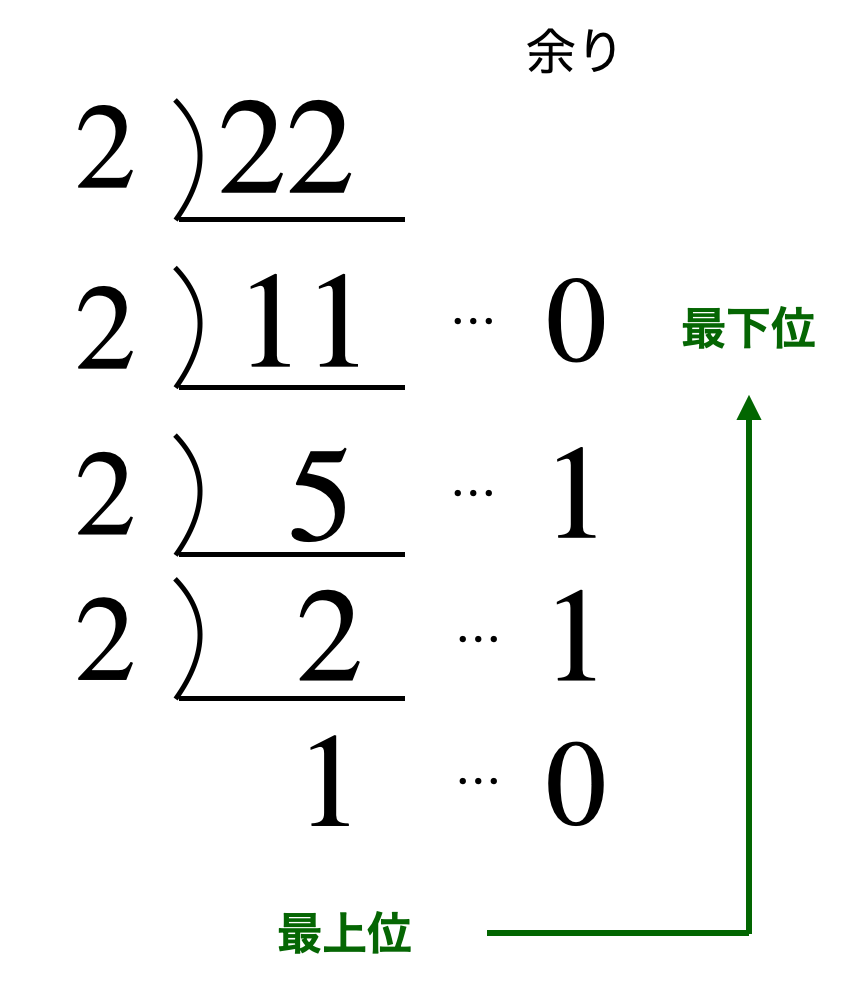
この計算の結果、$22_{(10)}=10110_{(2)}$となります。
2進数から10進数への変換は、2進数の各位に重みを掛け算した値を足し合わせることで可能になります。重みに関しては、n桁目の数字には$2^{n-1}$となります。
例として、$10110_{(2)}$の場合を考えます。

この表より、
$$1\cdot 2^4 + 0\cdot 2^3 + 1\cdot 2^2 + 1\cdot 2^1 + 0\cdot 2^0 = 22$$
となります。
2. 2進数の論理積(and, &)
論理積は、両方の数字が1なら1を返し、それ以外では0を返す計算です。
$$1\& 1=1, 1\& 0=0, 0\& 1=0, 0\& 0=0 $$
論理積を10進数の数字で計算する場合、各位の数字に対して(1)の計算を行います。
例えば、$10\& 8$の計算は、以下のように計算されます。
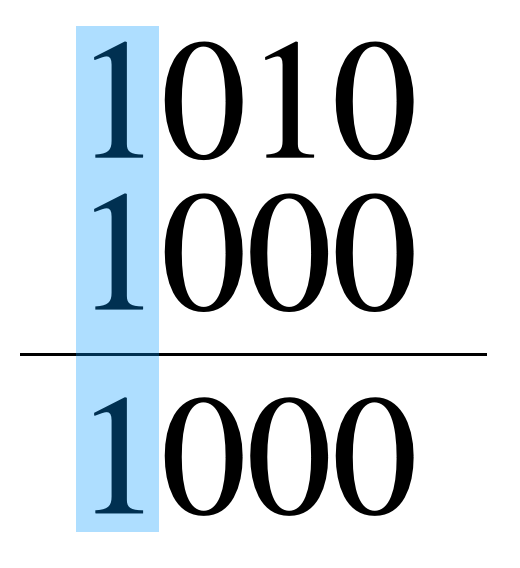
今回は$n\& 1$の形で使われますが、これはnを2進数表記の右端の数字が1かどうかを見ていることになるます。

3. 右シフト演算子
これは、2進数表記の数字を右方向にずらす操作を意味しています。
例として、$22 >>=1$を計算する場合を考えます。
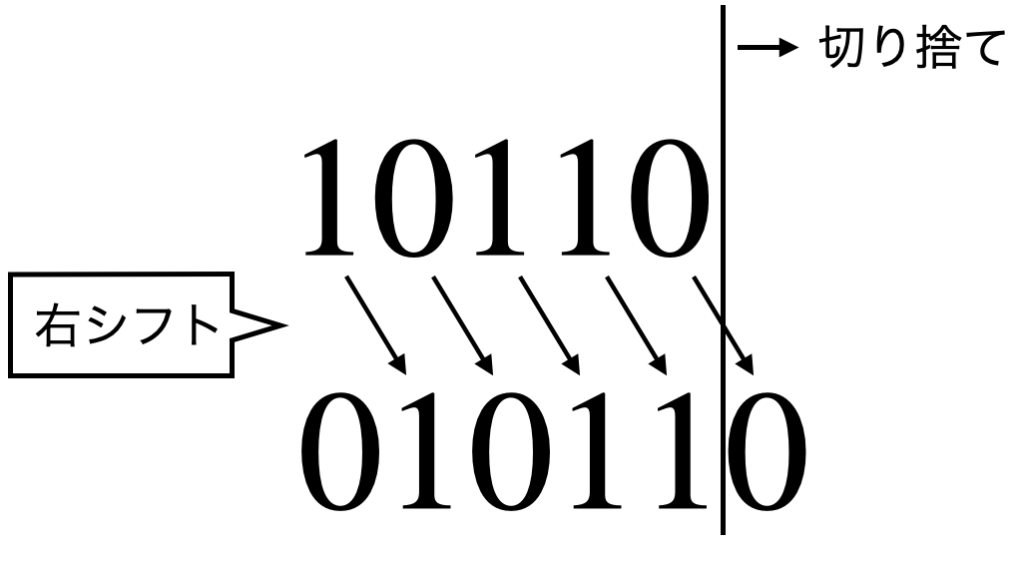
この計算の結果、答えは$01011_{(2)}=11_{(10)}$となります。
また、この計算は値を1/2倍する操作(余りは無視)と対応します。すなわち、$n=22$を一つ右シフトすると、$22/2=11$とすぐに値を計算できます。
繰り返し二乗法のコード
def pow(x, n):
res = 1
while n > 0:
#1. 2進数の論理積
if n&1: #(1)
res = res*x
x = x * x #(2)
#2. 右シフト演算子
n >>= 1 #(3)
return res$n$ を2進数で扱うと考えやすいと思います。
$$22_{(10)} = 10110_{(2)}$$
2進数->10進数に変換する場合、2進数の右から$i$個目の数字が1ならば$2^{2{^i}}$を足すことを繰り返します。(0-indexとします)
例えば、$n=22$の場合には以下のように計算できます。
$$22 = 2^4\cdot 1+2^3\cdot 0+2^2\cdot 1+2^1\cdot 1+2^0 \cdot 0 $$
この変形式を$x^{22}$に適用すると、
$$x^{22} = x^{{16} \cdot 1} \cdot x^{{8} \cdot 0} \cdot x^{{4} \cdot 1}\cdot x^{{2} \cdot 1}\cdot x^{{1} \cdot 0}$$
となります。
コードでは、1が掛け算されている項を抜き出し、変数 $res$ にかける処理を繰り返します。
コードの流れ
$n=22$の場合を例に、(1),(2),(3)の部分を中心にコードの挙動を見ていきます。
n=22の場合
(1): $22=10110_{(2)}$であり、最下位の数字は0です。そのため、$0\&1=0$となりif文は飛ばします。
(2): $x = 3*3 = 3^2$
(3): 右シフト演算子より、$n=11$となる。
n=11の場合
(1): $11=1011_{(2)}$であり、最下位の数字は1です。そのため、$0\& 1=1$となり、if文の計算をします。結果、$res = res * x = 9$ となる。
(2): $x = x*x = 3^4$
(3): 右シフト演算子より、$n=5$となる。
n=5の場合
(1): $5=101_{(2)}$であり、最下位の数字は1です。そのため、$0\& 1=0$となり、if文の計算をします。結果、$res = res * x = 3^2 * 3^4= 3^6$ となる。
(2): $x = x*x = 3^8$
(3): 右シフト演算子より、$n=10_{(2)}=2_{(10)}$となる。
n=2の場合
(1): $2=10_{(2)}$であり、最下位の数字は0です。そのため、$0\& 1=0$となり、if文の計算を無視します。
(2): $x = x*x = 3^{16}$
(3): 右シフト演算子より、$n=1$となる。
n=1の場合
(1): $1=1_{(2)}$であり、最下位の数字は1です。そのため、$1\& 1=1$となり、if文の計算をします。結果、$res = res * x = 3^6 * 3^16= 3^{22}$ となる。
(2): $x = x*x = 3^{32}$
(3): 右シフト演算子より、$n=0$となり、計算は終了となる。
答えは$3^22=31381059609$となり、正しく計算できていることが確認できました。
問題例
繰り返し二乗法を使う問題です。違いとしては、modの計算が含まれています。
まとめ
繰り返し二乗法に関してまとめました。この手法の理解には2進数や論理積、シフト演算の理解が重要となるため、簡単に解説も入れています。
以下の書籍を参考にしています。




コメント