トポロジカルソートとは
トポロジカルソートを一言で言うと、すべての有向辺の方向が左→右へ向くように頂点を並び替えることです。
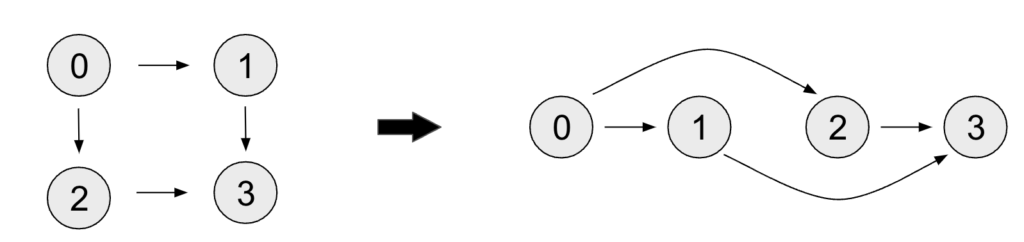
左のグラフをトポロジカルソートしたものが右のグラフ.全ての矢印を左から右へ揃えられている.
もしも閉路が存在している場合、いずれかの辺が左←右を向いてしまうため、トポロジカルソートができません。
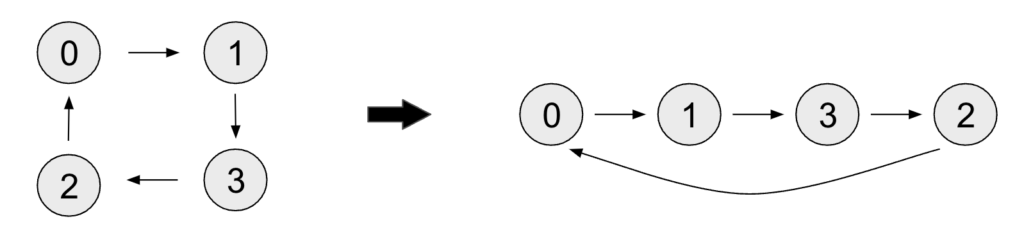
右の頂点2から頂点1のように、右から左への矢印が発生してトポロジカルソートできない.
そのため、トポロジカルソートのアルゴリズムは閉路の存在有無の確認にも利用することができます。
pythonでの実装
トポロジカルソートの実装には、幅優先探索を用いる方法と深さ優先探索を用いる方法の2種類存在します。今回は幅優先探索を利用して実装します。
from collections import deque
def topological_sort(G, into_num):
#入ってくる有向辺を持たないノードを列挙
q = deque()
#V: 頂点数
for i in range(V):
if into_num[i]==0:
q.append(i)
#以下、幅優先探索
ans = []
while q:
v = q.popleft()
ans.append(v)
for adj in G[v]:
into_num[adj] -= 1 #入次数を減らす
if into_num[adj]==0:
q.append(adj) #入次数が0になったら、キューに入れる
return ans
トポロジカルソートを実行する際のポイントは、ノードの入次数を管理するリスト into_num です。
実装コードのデモ
以下のグラフに対してトポロジカルソートしてみます。緑丸が頂点で、各頂点に0から5までの番号をふっています。矢印は有向辺です。
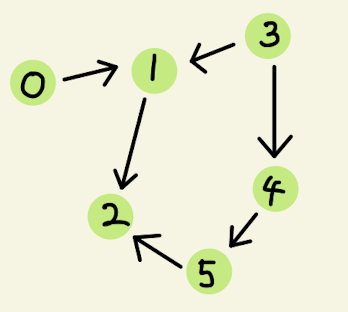
このグラフの隣接グラフと入次数リストは以下のようになります。
G = [[1], [2], [], [1, 4], [5], [2]]
into_num = [0, 2, 2, 0, 1, 1]これを上の自作コードでトポロジカルソートします。
ans = topological_sort(G, into_num) #トポロジカルソート
print(ans)
#[0, 3, 1, 4, 5, 2]閉路の存在有無の確認方法
トポロジカルソートされた順番の頂点番号のリストの長さが与えられた頂点数に一致しない時、もとのグラフに閉路が存在していることになります。
コードでかくと、
ans = topological_sort(G, into_num) #トポロジカルソート
#トポロジカルソートされたリストの頂点数 と 元のグラフの頂点数を比較
if len(ans)==len(G):
print('閉路なし') #同じ頂点数なら閉路なし
else:
print('閉路有り') #頂点数が異なると閉路が存在しているまとめ・参考
トポロジカルソートについて学んだことをまとめました。
今回書いたコードは、AIZU_ONLINE_JUDGE_GRL#4_B: Topological Sort で正解になることを確認しています。
また、以下の書籍も参考にしました。
『プログラミングコンテストチャレンジブック [第2版] 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える』, 秋葉拓哉、 岩田陽一、 北川宜稔, マイナビbooks, 2012年
『問題解決力を鍛える!アルゴリズムとデータ構造』, 大槻兼資・著 秋葉拓哉・監修, 講談社サイエンティフィク, 2020年

コメント