Union-Findというデータ構造をpythonで実装してみました。
Union-Findについて
Union-Findは木構造を持つデータ構造で、グループ分けを効率的に管理することができます。
例えば、以下のように0の球と1の球が同じグループ、2,3,4の球が同じグループにあったとします。
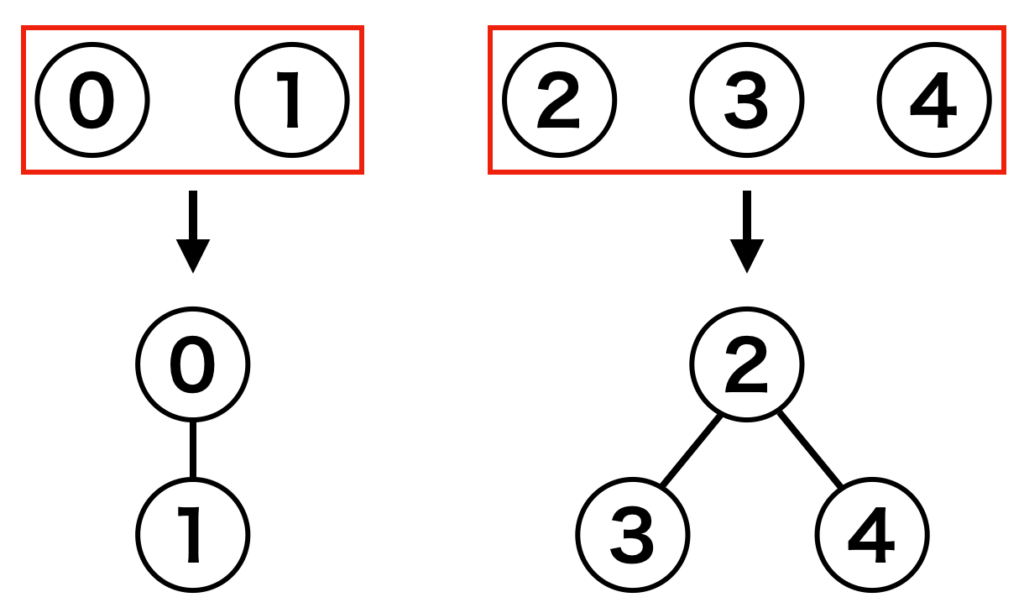
0の球と1の球が同じ分類に存在している場合、0の球の下に1の球を接続して木構造として管理するというのがUnionFind木のアイデアです。
言い換えると、『同じ集合に属すること=同じ木に属すること』と考えることができます。ほかの数字の球も同じように木として管理します。
Union-Findの部品について
このデータ構造には、以下の2つのリストが管理されます。
・parents : 各頂点の根の番号を管理するためのリスト。自身が根である場合は-1と定義する。
・size : 各頂点が属する集合の要素数(根付き木の頂点数)を管理するためのリスト。
上の絵をparentsで管理すると、以下のようになります。ただし、parentsのindexと球の番号が一致していると考えています。
parents = [-1, 0, -1, 2, 2] ##順番に0の球,1の球,2の球,3の球,4の球例えば、0の球は木の根(てっぺん)にあるので、parentsには-1が格納されます。1の球は0の球を根とする木に接続しているので、0が格納されます。
Union-Find木で用いる関数について
上記の2つのリストを管理するための関数として、以下の4つの関数が定義されます。
・root(x) : 頂点xを含む集合(根付き木)の根番号を返す関数
・isSame(x,y) : 頂点xと頂点yが同じグループに属しているかどうかを判定する
・unite(x,y): 頂点xを含む集合と頂点yを含む集合を合併して一つの集合にする
・Size(x) : xが属する集合(根付き木)の要素数を返す
Union-Findを高速化するための工夫
大きく2つの工夫が存在しています。
工夫1. サイズによる合併(小さい方を大き方に合併させること)
工夫2. 経路圧縮
1番目の工夫は、集合の要素数が小さい方の根を、大きい方の根にくっつけるというものです。
この工夫はunite(x,y)関数でsizeリストの比較している箇所に見られます。
xが集合の要素数が大きい方、yが集合の要素数が小さい方を想定しています。
def unite(self, x, y):
...略...
if self.size[x] < self.size[y]:
x, y = y, x #xとyを交換
self.parents[y] = x #yの根をxにする
self.size[x] += self.size[y] #xが属する集合の要素数をyyが属する集合の要素数だけ増やす
...略...もしも1番目の工夫をしなければ、以下のようにxとyの交換がなくなるようなコードになると思います。
def unite(self, x, y):
...略...
#f size[x] < size[y]:
# x, y = y, x #xとyを交換
self.parents[y] = x #yの根をxにする
self.size[x] += self.size[y] #xが属する集合の要素数をyyが属する集合の要素数だけ増やす
...略...2番目の工夫である経路圧縮はroot(x)関数のコードに見ることができます。
def root(self, x):
if (self.parents[x]==-1):
return x
else:
return self.parents[x] = self.root(self.parents[x]) #xの根parents[x]を集合の根に繋ぐもし経路圧縮を行わない場合は以下のようなコードになります。
def root(self, x):
if (parents[x]== -1):
return x
else:
return self.root(self.parents[x]) #再帰的にxが属する根に向かっていく一見するとなにも変わってなさそうにも見えますが、この微妙な違いで高速化できてしまうのは面白いです。
Union-Findのpythonコード
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1 for i in range(n)]
self.size = [1]*n
def root(self, x):
if self.parents[x] == -1:
return x
else:
self.parents[x] = self.root(self.parents[x]) #工夫2: 経路圧縮
return self.parents[x]
def isSame(self, x, y):
if self.root(x)==self.root(y):
return True
else:
return False
def unite(self, x, y):
x = self.root(x)
y = self.root(y)
if x==y:
#なにもしない
return
#工夫1: サイズによる合併(小さい方を大き方に合併)
if self.size[x] < self.size[y]:
x, y = y, x #yが小さい方になるように交換する
self.parents[y] = x #yの根をxに変更
self.size[x] += self.size[y]
def Size(self, x):
return self.size[self.root(x)]isSame(x,y) は頂点xの根 root(x) と頂点yの根 root(y) を求め、両者が同じであれば True, 異なればFalse を返します。
unite(x,y)でも、まず最初に頂点xの根 root(x) と頂点y根 root(y) を求めます。両者が異なれば別の木に属することになり、root(x) と root(y) を合併します。
root(x) と root(y) が同じ場合は、すでに同一集合に属していることを意味するのでなにもしません。
このように、isSame(x,y), unite(x,y) のいずれも root(x) 関数が中心的役割を担っています。
まとめ・参考
Union-Find木について解説をしました。
以下のリンク・書籍を参考にしました。



コメント