物体検出のモデルの性能評価指標の一つに、AP(Average Precision)があります。この指標の概要と計算方法に関してまとめます。
本記事の目標
- 4つのステップに分けてAPの概念の理解を目指す
- APの計算のためのpythonコードを理解する
IoU (Intersection of Union)について
簡単に言えば、矩形の重なり具合を数値的に表現した指標です。
$$\mathrm{IoU} = \frac{A \cap B}{A \cup B}$$
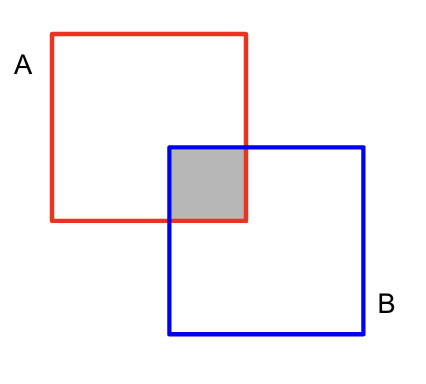
上の例からIoUを求める際、
$$IoU=\frac{灰色の面積}{Aの面積+Bの面積-灰色の面積}$$
とすることで具体的な値を計算することができます。
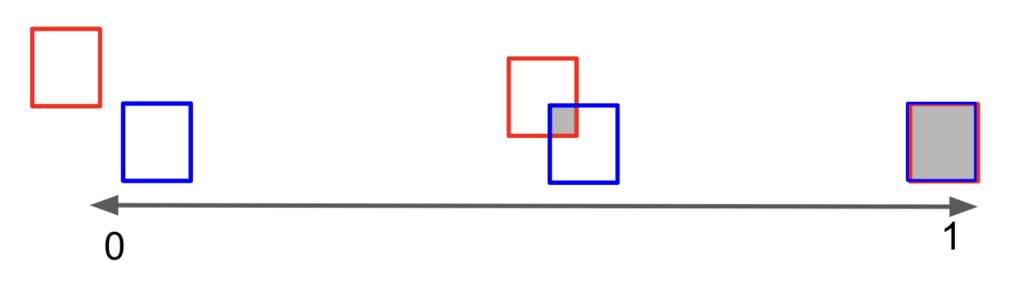
数値は0-1の間をとります。1は完全に重なる状態で、0には重なりが全くない状態を意味します。
物体検出におけるTP, FP, FNについて
TP, FPを物体検出で考える場合、『IoUの閾値』と『見検出かどうか』の2つの条件で決定されます。
- TP (True Positive): 『モデルの予測矩形とGTとのIoUが閾値以上』かつ『GTがまだ他の予測矩形と紐付いていない』
- FP (False Positive): TPの条件を満たさない予測矩形
- FN (False Negative): どの予測矩形ともIoU以上の重なりを持たなかったGT
と定義されます。
例として、以下のようにGT2個(赤四角)と予測矩形(黒四角)2個の場合を考えてみます。IoUの閾値は0.5とします。
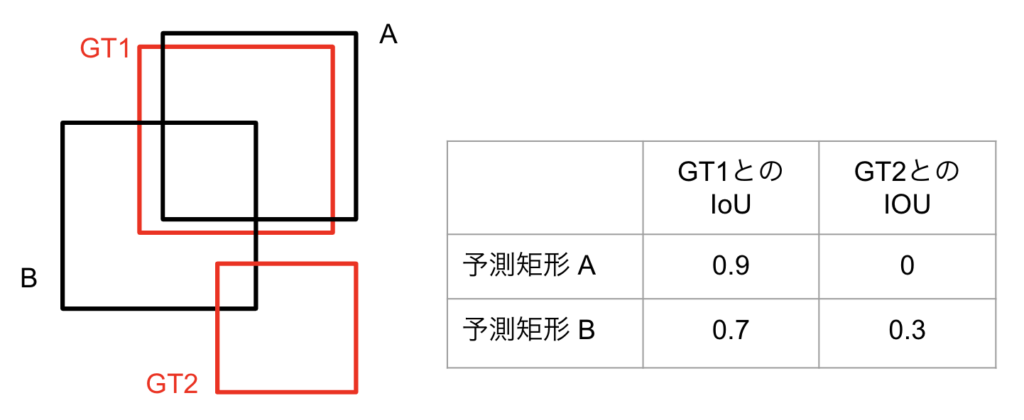
- 予測矩形AとGT1を見ると、IoUは0.9 かつ GTが他の予測矩形と紐付いていないため、Aは正解となる。
- 予測矩形BとGT1を見ると、IoUは0.7だがGTがAと紐付いているため、Bは不正解となる。
- 予測矩形BとGT2を見ると、IoUの閾値に満たないため、不正解となる。
従って、 $\mathrm{TP}=1, \mathrm{FP}=1, \mathrm{FN}=0$と計算できます。
Precision(適合率)とRecall(再現率)
$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP + FP}}$$
$$\mathrm{Recall} = \frac{\mathrm{TP}}{\mathrm{TP + FN}}$$
適合率と再現率を一言で言うと、
- 適合率: 全判定のうち、正解だった割合
- 再現率: 全正解のうち、モデルに判定された割合
となります。
図3の例を用いると、
$$\mathrm{Precision}= \frac{1}{2} = 0.5$$
$$\mathrm{Recall}= \frac{1}{2}=1$$
と計算できます。
Precision-Recall曲線
これはPrecisionを縦軸、Recallを横軸にしてプロットしたグラフです。
PR曲線を描くため、以下のようにGroundTruth 4個の場合を例にして考えてみます。
これらのGTに対し、6個の矩形が判定されたとします。
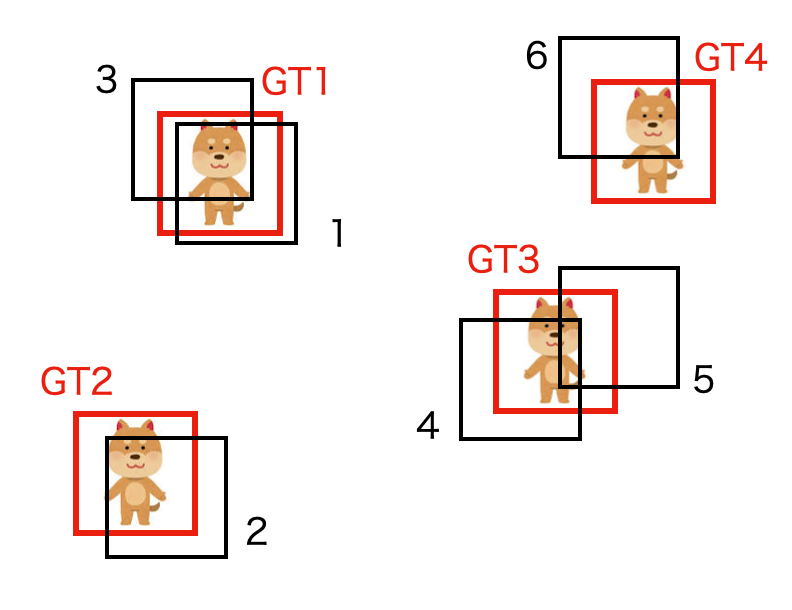
まず6個の予測矩形を信頼度が高い順に並べ、予測矩形が正解か否かを調べます。
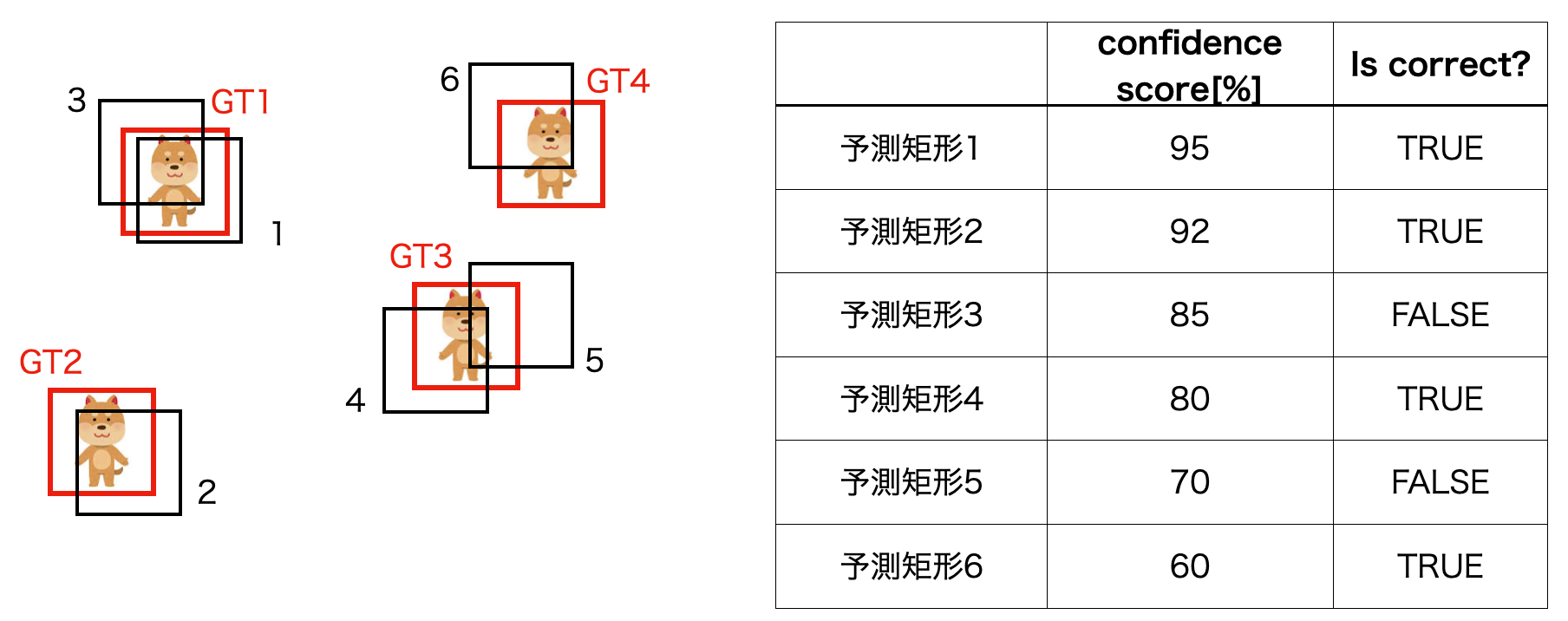
この表の TRUE, FALSE を用いてTP,FPを計算します。
# "Is correct?"の列をpandasのデータフレームで扱う
correct = pd.Series([True, True, False, True, False, True])
TPs = correct #[True, True, False, True, False, True]
FPs = ~correct #[False, False, True, False, True, False]次に、TPs, FPs を用いて Precision, Recall を計算します。
#累積和
accTP = TP.cumsum() # [1, 2, 2, 3, 3, 4]
accFP = FP.cumsum() # [0, 0, 1, 1, 2, 2]
#Precision, Recallの計算
numGT = 4 #GroundTruth の個数
precision = accTP / (accTP + accFP)
recall = accTP / numGT #分母はGTの個数最後に、上で得られた Precision と Recall を使ってグラフを作成します。
plt.plot(recall, precision)
plt.scatter(recall, precision, color="b")
plt.grid()
plt.xlabel("Recall")
plt.ylabel("Precision")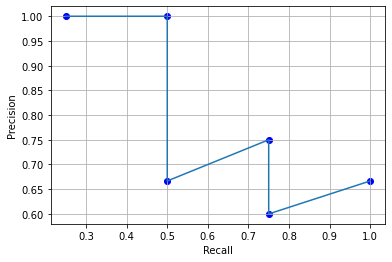
APの定義と計算方法
ついに AP(Average Precision) の計算になります。
APの公式は、以下で表されます。
$$\mathrm{AP} = \int_{0}^1 P(r)dr$$
ただし、$r$はRecallの値(横軸の値)で$P(r)$はRecallが$r$の時のPrecisionの値を意味します。
簡単に言えば、PR曲線下の面積がAPです。
実用上は、離散データしかないため、以下の式で計算されます。
$$\mathrm{AP} = \sum_{i=2}^N (r_i – r_{i-1}) P(r_i)$$
APを計算するために、以下のステップを踏みます。
- 横軸を[0,1]へ拡張
- PR曲線を階段関数に変換
- APの計算
横軸を[0,1]へ拡張
積分の範囲が[0,1]なので、それに合わせてrecall, precisionを調整します。
#1. 横軸を拡張
extend_recall = np.concatenate([[0],recall,[1]])
extend_precision = np.concatenate([[0], precision, [0]])階段関数に変換
ジグザクのパターンを階段関数へ変換します。
# 2. 階段関数に変換
step_func = []
val = 0
for p in precision[::-1]:
val = max(val, p)
step_func.append(val)
plt.plot(extend_recall[1:], extend_precision[1:], lw=3) #青色曲線
plt.plot(extend_recall, step_func[::-1], color='#ff7f00', linestyle = "dotted", lw=3) #オレンジ色 階段関数
plt.scatter(extend_recall, step_func[::-1], color='#ff7f00') #
plt.grid()
plt.xlabel("Recall")
plt.ylabel("Precision")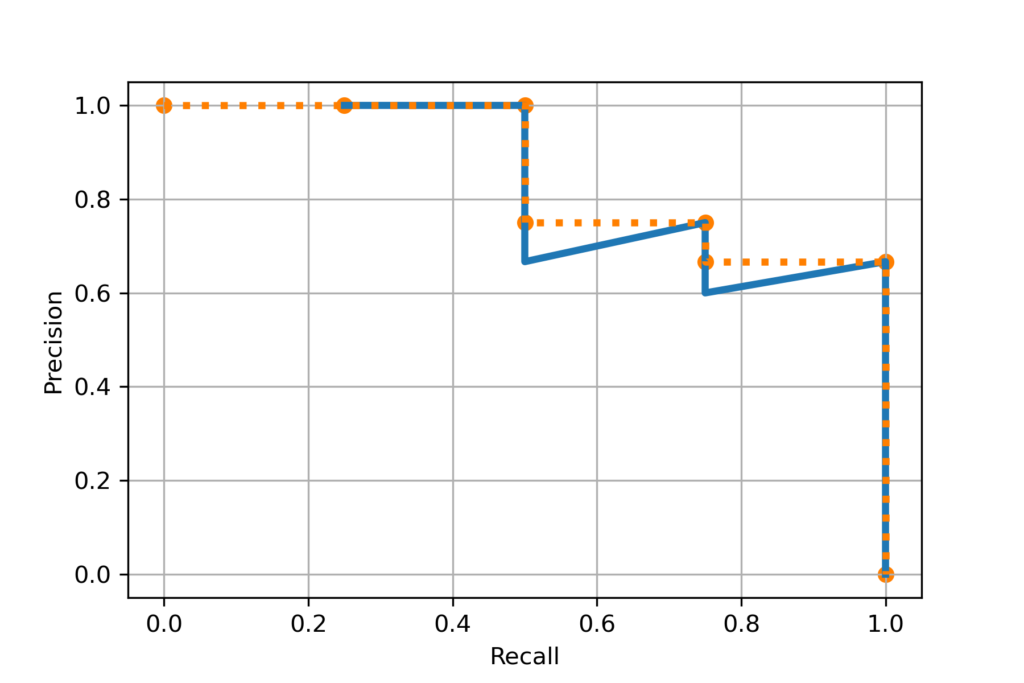
APの計算
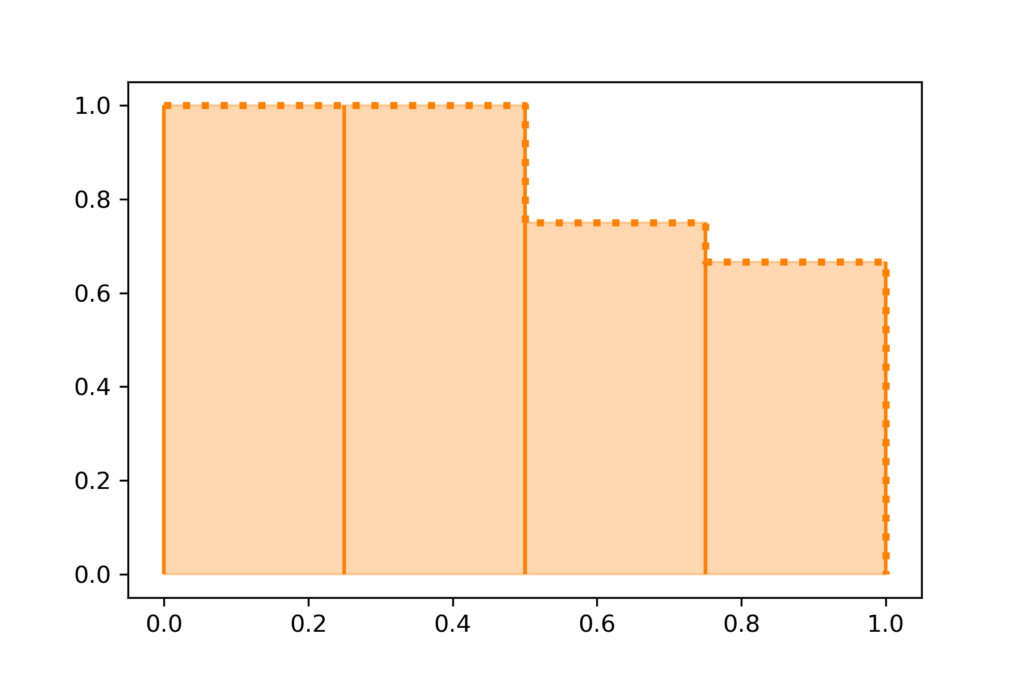
オレンジ色の階段関数の面積がAPとなります。
$$\mathrm{AP} = \sum_{i=2}^N (r_i – r_{i-1}) P(r_i)$$
階段関数として計算するため、下のグラフのように長方形の面積の総和としてAPを計算できます。
ap = 0
for i in range(1, len(extend_recall)):
dr = extend_recall[i] - extend_recall[i-1]
ap += dr * precision[i]
print(ap) #APの計算結果
#0.8541666666666666まとめ
AP(AveragePrecision)に関して学習したので、内容をメモとして残しました。APの理解には、以下の項目の理解が重要です。
- IoU
- 物体検出におけるTP,FP,FNの計算方法
- 適合率(Precision), 再現率(Recall)の概念
- PR曲線と面積の計算
また、学習において参考になった記事もいくつか紹介します。


本記事が少しでも参考になれば幸いです。